Reverse Engineering the Human Brain
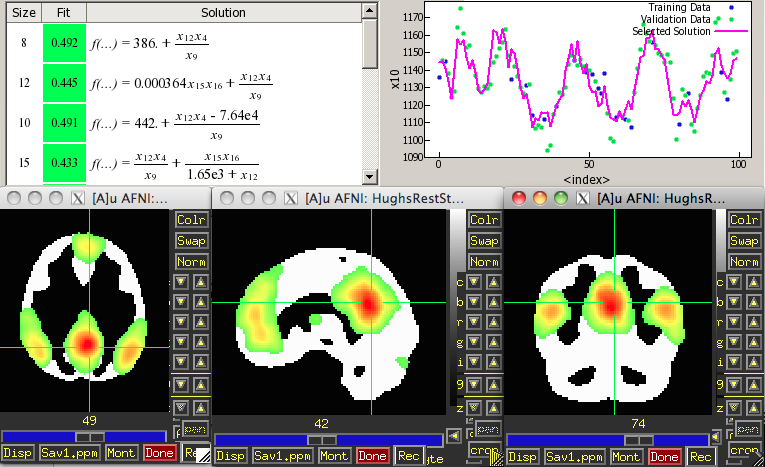
A detailed characterization of the human brain, its structural and functional underpinnings, remains on the frontier of modern science. Neurological research is important not only for its intrinsic interest, but for the purpose of better understanding (diagnosing and treating) neurological disorder as well. Happily, along with many other fields, neuroscience is entering an era of "Big Data" in which a new approach is possible: analyze the data, using some new and exciting computational methods, to generate hypotheses about brain function, which can then be tested on independent data. Using data from functional Magnetic Resonance Imaging (fMRI), and computational techniques inspired by biological evolution, we attempt to discover interactions among regions of the brain while a subject is either at rest, or performing certain tasks. This approach allows the discovery of meaningful information about brain function that an MRI researcher might not hypothesize directly. Futhermore, the method makes no linear assumption, and can thus uncover brain function not discoverable by standard analytic techniques.
Check out this poster summarizing some of my recent work in this area, or read about some previous (and prelimineary) exploratory work detailed in a conference-style paper (not published) that can be found here: Reverse Engineering the Brain with Eureqa.
Weather and Climate Forecasting
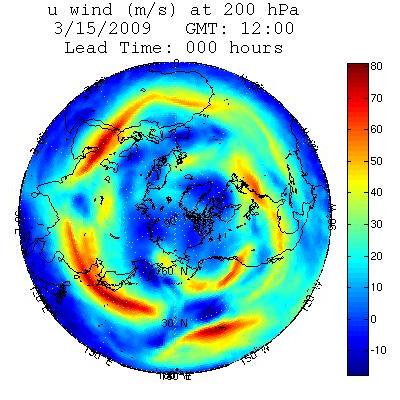
The chaotic nature of the Earth's atmosphere drives weather forecasts away from reality at an exponential rate, leading to much worse predictions at 3-days than at 3-hours. Even very small errors are magnified drastically over time, which underlines the importance of accurate initial conditions. However, even with perfect estimates of the state of the atmosphere, discrepancies between nature and our models would still produce the runaway effect of chaos. I am investigating a principled approach to the mitigation of those discrepancies. By comparing initial conditions from the last half-century to the forecast errors they generate, the error tendencies of the model can be determined mathematically. Those tendencies can then be counteracted at every step, significantly reducing errors. In addition to this step-by-step correction, it may be possible to determine what component of the model is at fault for a specific error pattern and remove the biased tendency altogether. This technique is being tested on the operational Global Forecast System (GFS) weather model used by the National Weather Service, which has approximately one billion degrees of freedom. If successful, the methodology will be used to improve forecasts of the Earth's climate as well.
Some MATLAB-generated visualizations of data produced by the GFS:
Animations: Zonal Wind Heat Flux Pressure TemperatureWind Stills: Initial State 6-Hour Error 3-Day Error 10-Day Error
publication
I have a manuscript published in Physical Review E covering the application of empirical correction to a simpler system. A local copy can be accessed here: Empirical correction of a toy climate model. Or take a look at this poster summarizing that work.
Complex Networks
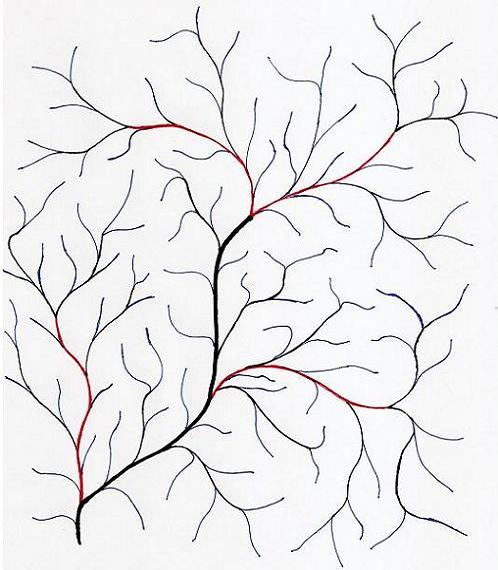
Many real-world systems, natural and man-made, can be modeled by graphs in which the vertices, or nodes, are entities in the system and edges between nodes represent relationships between entities. Edges can be weighted or directed to more adequately characterize relationships, but in the simple case, every edge has weight 1 and no direction. These graphs, and the systems described by them, are often called networks. Examples of such systems include the national power grid, the Internet (and world-wide web), ecosystems, social or political networks, protein interaction and gene regulatory networks. There has been an explosion in the study of network structure not only because of its ubiquity, but also due to the relatively new availability of mountains of data on these real-world systems. The search for metrics with which to describe and categorize networks based on data about their structure is in full swing, and my particular interest is in the evolutionary mechanisms at work in these systems. Specifically, to what extent can we characterize the historical dynamics of a network from its current structure, and how might we do that? This is an important question because we often do not have historical data.