4 Objects
In addition to entering functions in R, you will create and edit “objects”. . . tons of them . . . in all different sizes, shapes, and flavors. This chapter will introduce you to objects in R. Warning! This is a long chapter. You don’t have to memorize anything, and we encourage frequent breaks. The goal here is to make you realize that there are many kinds of objects and many kinds of datatypes, and that there are a few key functions that can help you know what kind of object you are dealing with. We’ll be working with objects extensively in future chapters . . for now, breathe easy and try to keep the big picture in mind.
Open a new R script file and save it as chapter4.R in your R_for_Fledglings directory. Use this script for all of this chapter’s work.
In Chapter 3 we used the sqrt function to calculate the square root of a number. That was neat, but it would be nice to save the result for later.
Creating a new object is as easy as typing the object’s name and assigning a value to it. There are multiple ways to assign values to objects in R. As in many computer languages you can use the equal sign (=) as an assignment operator. Copy the following code into your script, and run it.
Now we have created an object called result. To verify that, we can type the name of the object, and R will print the value stored for it (emphasizing that an object has a name and a value):
## [1] 10You can replace these two lines of code with one by wrapping the result = sqrt(100) within parentheses. This creates the object “result” and returns the result.
## [1] 10In this book, we won’t be using the = sign to create objects in R. Instead, we’ll be using the more conventional the left-pointing assignment arrow to create our objects, which looks like this <-. The downside is that we have to type twice as many characters (small con), but the upside is that the directionality of the assignment (name <- value) is clear (big pro). You can also use a right-pointing assignment arrow to create objects. However, the left-pointing arrow is preferred because it allows us to name the object first, then assign any value to it. In this way, object names are always located along the left margin, which makes our code easier to read, especially when it comes to locating objects within the code.
You can easily create this arrow in RStudio by pressing Alt and dash keys simultaneously (Alt+-). More keyboard shortcuts can be found in the Help menu.
## [1] 10Now, let’s remove this object from our global environment:
Let’s bring it back to life, this time with the assign function:
# use the assign function to create an object whose name is result and whose value is 10
assign(x = 'result', value = 10)
# look at the object
result## [1] 10Thus, <- and = invoke the assign function. You can learn more about assignment operators with this code:
You can think of an object in R as if it is a shoebox (object) with a name. Here, the name of the shoebox is “result”, and you can imagine that it is holding a scrap of paper with the number 10 on it. You can name your object (shoebox) anything you want (with a few exceptions), and you can store any value in it (with a few exceptions). For instance we could have named it Tintin if we wanted, but that wouldn’t have been very informative. The most important thing when naming an object is to assign a name that describes its contents and that you can remember later. Perhaps we should have named it sqrtResult. Stay clear of giving your objects names that are names of functions or any key words that seem like computer code, like “break”, “else”, “if,”for“,”TRUE“,”FALSE", etc.
Now lets change the value of our object.
## [1] 5Now you see that our “shoebox” named result has a different scrap of paper in it that has the value 5. Notice that we have replaced our first result (10) with the new result (5). R does not give a warning that the current value will be overwritten. If you really want to store the first result, you might change the name of the second result to result2.
An object doesn’t have to be a single value. In fact, as we’ll soon see, objects come in many shapes, sizes, and flavors. For example, if we want to create an object called lowNumbers that stores the numbers 1, 2, 3, 5, and 6 as a single group that skips the number 4, we would enter into our console:
# create an object called lowNumbers, and make it a vector with the numbers 1, 2, 3, 5, and 6
lowNumbers <- c(1,2,3,5,6)
# look at the object called lowNumbers
lowNumbers## [1] 1 2 3 5 6We used the c function (combine function) to combine the numbers 1, 2, 3, 5, and 6 into a new shoebox (object) called lowNumbers, which has a single scrap of paper with the numbers 1, 2, 3, 5, and 6 in that order. If you use spreadsheets, this is analogous to entering the same numbers in cells A1 through A5 and then naming the entire range A1:A5 “lowNumbers”.
In R, we can also assign objects the value of other objects. If we want to add a new object fiveNumbers that has the same value as our object lowNumbers, we would write the declaration as follows:
Now let’s look at both objects:
## [1] 1 2 3 5 6## [1] 1 2 3 5 6To retrieve an object, just type the name of the object and send it to the console. A little trick to save some typing is to use your tab key . . . enter the first letter of the object, then press tab. A small dialogue box will open that displays objects (including functions). Below, we typed in “r”, then pressed “tab”. Do you see the object called result? You may have scroll a bit. Objects that can be selected are color-coded: functions are light blue, objects are coded in pink, packages have purple P, and dataframes look like a tiny grid. If you press tab again, the highlighted word is inserted.
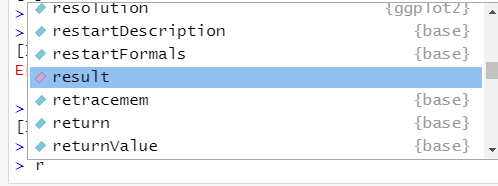
Figure 4.1: The tab key in RStudio is super helpful!
4.1 The Global Environment
Any objects that we create must live somewhere in R. Our objects, fiveNumbers, result, and lowNumbers all live in the global environment. Functions within packages all live in their own package environment.
Although the code below is overkill, it illustrates the fact that objects in R must exist in some environment or other, and that everything that R does is accomplished by a function, even if it happens behind the scenes:
## [1] 5In R Studio, click on the Environment tab in the upper right pane, and you’ll see your objects there. You can look at your objects in list view or grid view. Look for this toggle in the upper right hand corner of the Environment Pane, just above the search box: or
Your “list view”" should look something like this:
Figure 4.2: The list view.
And the “grid view”" should look something like this:
Figure 4.3: The list view.
You can use either view, but the grid view shows more information about your objects, and you can select individual objects. The columns within the grid view include:
- Name = name of the object.
- Type = type of the object (its mode is shown if the object is a vector; its class is shown if the object is more complicated that a simple vector).
- Length = length of the object.
- Size = size of the object (in terms of digital information).
- Value = current value of the object (what’s in the shoebox).
As we’ll soon see, the column “Type” can be confirmed with the mode function for simple objects (like vectors) or with the class function for more complex objects.
Let’s look at the objects we’ve created in grid view.
We’ve created an object called result, which if you recall, holds the result of the sqrt function we used earlier. The name of this object is result, and it is a number. It’s current value is 5, and R is using 48 bytes of memory to store this number. It has a length of 1 because it stores a single number.
We also created an object called fiveNumbers, which if you recall, is a vector that contains the numbers 1, 2, 3, 5, and 6 in that order. The name of this variable (or object) is fiveNumbers, and the type of information stored in this vector is numeric.
## [1] "numeric"It has a length of 5 because it stores 5 numbers. R is using 88 bytes to store this object (your result may be a bit different). Under the column “value”, we see num[1:5] 1 2 3 5 6. This is very informative; it tells us that R is storing this object as a vector – a type of object that stores a series of items such as a single row or single column in a spreadsheet. Specifically, the notation [1:5] tips us off that this object is a vector that contains 5 elements (cells). The num notation preceding it indicates that the values stored are numbers (or numeric mode). Then we see the actual values stored within fiveNumbers, which are 1, 2, 3, 5, and 6.
We’ve mentioned that the Environment tab is the Most Valuable Player (MVP) of RStudio. There is no faster way to learn how to code in R than to execute some code, and then look in the Environment pane and see what happened.
4.2 Data Types (Modes)
We now have a few different objects in our global environment, but how exactly does R store them for future use? In this section, we’ll learn about the most commonly used ‘data types’ or storage modes in R. These include dates, numbers (integers and decimals), and logical (true/false) values.
Let’s create a new vector called fiveRandoms which will be a vector that stores 5 random numbers between 0 and 1, drawn from a uniform distribution. In Excel, this is done by using the RAND function. In R, this function is called runif, which stands for “random uniform”. First, let’s look at the helpfile.
And now we can create our new object.
# create a new object called fiveRandoms, using the runif function
fiveRandoms <- runif(n = 5)
# look at the object called fiveRandoms
fiveRandoms## [1] 0.8573828 0.3514372 0.1363997 0.4367107 0.1694715Your random numbers will be different than ours (more on that later).
Now let’s look at the object in the Environment pane. You should see that fiveRandoms also have a numeric type, which is its mode.
Now let’s use the sample function to randomly sample 5 numbers between 1 and 100. It’s important here to look at the helpfile, and to understand each argument.
## function (x, size, replace = FALSE, prob = NULL)
## NULLThis function has four arguments: x is a vector you’d like to sample from, size is the number of samples to take, replace indicates whether you’d like to sample with replacement (which means the same numbers can be drawn repeatedly), and prob is used when you want to weight your samples so that some have a higher chance of being selected than others.
Now that you’ve scanned the helpfile and arguments, we can create our object. We’ll draw 5 random samples (with replacement) from a vector containing the numbers 1 through 100. Don’t forget the tab trick for entering function arguments! It should be clear that x, size, replace, and prob are the names of the arguments for the sample function.
# create a new object called fiveIntegers, using the sample function
fiveIntegers <- sample(x = c(1:100), size = 5, replace = TRUE)
# look at the object called fiveIntegers
fiveIntegers## [1] 60 2 45 20 99Now take a look in the Global Environment at this new entry. You should see a new entry under the column Type called integer. Numeric modes include both “integers” and “double”, and RStudio is displaying this more fine-grain information.
If the Environment tab is the MVP of RStudio, the str function is the MVP of R functions for learning about objects.
## num [1:5] 0.857 0.351 0.136 0.437 0.169## int [1:5] 60 2 45 20 99The str function returns the structure of an object in the R console, where it confirms that our object, fiveRandoms is indeed a vector of numbers, and that our object, fiveIntegers, is indeed a vector of integers. Remember that the notation [1:5] indicates that our objects are vectors. We’ll be using the str function repeatedly in this primer.
What about dates? Let’s try it. The function that returns today’s date and time is the date function, with no arguments:
## chr "Wed Feb 10 10:13:16 2021"What happened here? The object called today is stored as a character (also called a “string” or “text” in other computer languages). The str function indicates this by returning chr, while the word character is displayed in the global environment for this new object. Both suggest the same thing: R is storing the object called today as a string of characters. Objects that are characters can be spotted from afar because the values are in quotes.
Let’s enter the birthday of Nelson Mandela:
## num 0.000203Now it is clear that if you want to enter a date into R you have to be careful, or R will think you are using it as a calculator! Here, R returned 7 divided by 18 divided by 1918. You can force the birthday object to be a date by using the as.Date function:
# use the as.Date function to convert Nelson Mandela's birthday to a date
birthday2 <- as.Date("7/18/1918")Error in charToDate(x) :
character string is not in a standard unambiguous formatHmmmm . . . R returned an error indicating that the character string “7/18/1918” is not in a standard unambiguous format. That is to say, “7/18/1918” is ambiguous and R doesn’t know how to read it. Dates can be written in so many different ways! We need to tell R how our date is formatted.
# this would work because we tell R how the original date was formatted
birthday2 <- as.Date("7/18/1918", format = "%m/%d/%Y")
# look at the structure of birthday2
str(birthday2)## Date[1:1], format: "1918-07-18"Let’s try another approach that uses ISO 8601 standard. This is the default date standard in R. The Wikipedia site indicates “The purpose of this standard is to provide an unambiguous and well-defined method of representing dates and times, so as to avoid misinterpretation of numeric representations of dates and times, particularly when data is transferred between countries with different conventions for writing numeric dates and times.” The ISO format is easy to remember because it goes from the largest time scale (years) to the smallest (days), or year-month-day.
# use the year-month-day format, which is R's default
birthday2 <- as.Date("1918-07-18")
# look at the structure of birthday2
str(birthday2)## Date[1:1], format: "1918-07-18"Now look in the Environment pane, and you should see a Date datatype associated with birthday2 while birthday (our first attempt) has a numeric datatype. The output Date[1:1] indicates that birthday2 is a vector of length 1, and that this vector holds dates. We’ll learn more about dates when we work with our Tauntaun dataset.
Figure 4.4: The grid view.
The next datatype (storage mode) you should know about is called a “logical” datatype. Let’s create a new vector called fiveBooleans that contains only the words, TRUE or FALSE, by asking R if the random numbers contained in fiveRandoms are greater than 0.5. We do that by simply entering fiveRandoms > 0.5, which is another example of vectorization: R will evaluate each entry in fiveRandoms, and return the word TRUE if the entry is greater than 0.5 and FALSE if not.
## [1] TRUE FALSE FALSE FALSE FALSEVectorization is an R specialty . . . it allows rapid calculation across each element within an object without the use of loops (a topic covered in later chapters).
Your result will be different than the one listed above because your fiveRandoms object contains different values. If you look at the global environment, you should see that an object called fiveBooleans has been created, and this is a vector of length 5 with a type that is logical. This means it is a vector that contains only TRUE or FALSE entries. Note that TRUE and FALSE are capitalized. In other programming languages, this is known as a “boolean” data type.
We can also create an object of character data type. We’ve already seen that the object we created called today stores character data, but let’s look at another example. R has a built-in object called letters, which stores the letters of the alphabet. Let’s take a look at the letters object, and then assign a new object called letters2 to it:
# look at R's built in object called characters;
# note that this is not in your Environment
letters## [1] "a" "b" "c" "d" "e" "f" "g" "h" "i" "j" "k" "l" "m" "n" "o" "p" "q" "r" "s" "t" "u" "v" "w" "x" "y" "z"# create a new object called letters2
# set the value to be equal to the value in the object called letters
letters2 <- letters
# get the structure of the object, letters2
str(letters2)## chr [1:26] "a" "b" "c" "d" "e" "f" "g" "h" "i" "j" "k" "l" "m" "n" "o" "p" "q" "r" "s" "t" "u" "v" "w" "x" "y" "z"Look at the letters2 object in the Environment pane; you will see that it is a character type with a length of 26. Also note that each letter is enclosed by quotation marks. Further note R’s display of the letters in the console (yours may look slightly different). Do you see how the first line of output starts with [1]? This means that the returned output begins with the 1st element of the vector. Depending on your screen, your output may spill over into a second line. When multiple lines of output are needed to display the full vector, R tries to help us understand where we are in the vector by providing the “index” associated with the first entry on each line of output.
Can a vector store different types (modes) of data within it? Let’s try it. Create a new object (shoebox) called mixed, that contains 3 elements: “dog”, 10, and TRUE. Here, “dog” is a character, 10 is an integer, and TRUE is a logical datatype. Incidentally, R lets you write “dog” (with a double-quote), as well as ‘dog’ (with a single quote) . . . either is fine as long as you match them . . . both may be necessary if you are nesting quotation marks (e.g. bond <- ‘he said “shaken, not stirred”’ requires different types of quotation marks.
# create an object called mixed, with values "dog", 10, and TRUE
mixed <- c("dog", 10, TRUE)
# look at the object called mixed
mixed## [1] "dog" "10" "TRUE"You should see that R stores this vector as a character data type. Notice that the number 10 is actually stored as “10”, and the word TRUE is now stored as “TRUE”. The quotation marks around each element is a dead give-away that the object is a character type. Since “10” is now a character, it cannot be used as a number in calculations.
A vector must contain a single data type, and while it is possible to store the number 10 as a character type, it is not possible to store “dog” as a numeric type.
Let’s try another vector with mixed data types:
# create an object called mixed2, with values FALSE, 10, and TRUE
mixed2 <- c(FALSE, 10, TRUE)
# look at the object called mixed2
mixed2## [1] 0 10 1In this case, R stores the vector named mixed2 as a numeric type. What happens here is that the logical entries are interpreted as 1’s or 0’s, with TRUE equal to 1 and FALSE equal to 0.
Figure 4.5: The grid view.
The type (mode) of an object tells us how R is storing its content. A related function is called class, which returns the class of an object (which in turn controls how other functions work with the object).
## [1] "numeric"The class can also be inferred with the str function: the num output tells us the data are numeric, and the [1:3] output tells us the object is a vector (more on vectors in a minute).
## num [1:3] 0 10 1In our experience, one of the most common mistakes when coding in R occurs when trying to execute a function on objects of a given class when R is expecting something else. The str function is one of your best friends when it comes to R functions; it provides the class and a peek at the values as well.
Note: An object can be fully examined by using the
classfunction, thetypeoffunction, and themodefunction. Though not always the case, these three functions can return the same result, especially for vectors. We won’t dwell on the differences, but generally speakingtypeofandmodeprovide information about how R is storing an object, while an object’sclassdetermines how it is used in future R calls.
4.3 Changing Data Types
You were just introduced to a number of different data types that can be used in R. One of the neat / nice / convenient things about R is that if you don’t specify a data type, R will guess and assign the type it thinks best one that fits the data (as we saw with mixed value data).
However, there are times when R will guess wrong (particularly when reading data into R), and there are other times when we need a specific data type for the task at hand. For those times, R has coercion functions, which are generally used to convert an existing object to a new type as opposed to creating a new object. Coercion functions start with “as.” and end with the output class. Here are a few that convert objects from one type to another:
as.character- converts to character data typesas.numeric- converts to numeric data typesas.Date- converts to datesas.factor- converts characters to factors
Let’s practice one of these functions. Let’s practice using one of these functions by creating an object that stores Eleanor Roosevelt’s birthday as a string. Then we’ll change it to both a date data type and a numeric data type:
# create a character string of Eleanor Roosevelt's birthday
eleanor <- "1884-10-11"
# look at the value of eleanor
str(eleanor)## chr "1884-10-11"## Date[1:1], format: "1884-10-11"## num -31127We bet you weren’t expecting this answer! We’ll cover dates and what -31127 actually means in future chapters (yes, computers store dates as numbers).
R has another data type that we have not mentioned, the factor datatype. Factors look like characters, but they are not stored as characters . . . hence they can be a source of confusion. Factor datatypes are very important if you are planning to do statistical analysis on a dataset, such as a t-test or ANOVA. The easiest way to introduce you to factors in R is to create a vector of characters, change it to factors, and then discuss it.
# create a names vector of the boys in Mrs. Smith's first grade class;
# note how popular the name "Ben" is in Vermont
boys <- c("Ben", "Alden", "Ben", "Ben", "Max", "Elias", "Evan", "Miles")
# look at the structure; notice that this is a character vector
str(boys)## chr [1:8] "Ben" "Alden" "Ben" "Ben" "Max" "Elias" "Evan" "Miles"# convert the vector to factors
boys <- as.factor(boys)
#look at the structure, notice that this is a factor with 6 levels
str(boys)## Factor w/ 6 levels "Alden","Ben",..: 2 1 2 2 5 3 4 6Here an observant user may notice that factors are typically character values, but appear to be stored as an integer code in which each unique integer represents a longer character value. For example, the vector ‘boys’ is of class factor with 6 levels (unique values): “Ben”, “Alden”, “Max”, “Elias”, “Miles”, and “Evan”. From our output, it appears that “Ben” is stored as 2, “Alden” is stored as 1, “Max” is stored as 5, “Elias” is stored as 3, “Evan” is stored as 4, and “Miles” is stored as 6. Thus, each name is mapped to an integer that is stored internally by R. It appears that R has assigned these numbers alphabetically.
The levels functions returns the names of each level.
## [1] "Alden" "Ben" "Elias" "Evan" "Max" "Miles"Note that this returns the common name in the order of their numeric assignment, but does not provide the numeric assignment directly. If you want to see the integer mapping, use the as.integer function:
## [1] 2 1 2 2 5 3 4 6The take home point is that R is storing the factors as numbers behind the scenes, but there is usually no need to convert factors to integers.
If you want more control over how the mapping from levels to integers is done, use the factor function. In this next example, let’s suppose that you have some integer data from 1:5, and these designate people’s ratings of “Cosmos” on Netflix. Here, we’ll use the sample function to create a dataset called data that consists of 50 viewer ratings. We’ll draw 50 random samples with replacement between 1 and 5, and include the prob argument to establish the probabilities of drawing each number. The use of the ‘prob’ argument can be used to weight how the numbers are drawn . . . in the code below, there is a 0 probability of drawing a score of 1, a 10% chance of drawing a score of 2 . . . and a 60% chance of drawing a 5. “Cosmos” is a great series!
# create a dataset with 50 values of numbers of 1 to 5 using the sample function;
data <- sample(x = 1:5, size = 50, replace = T, prob = c(0, 0.1, 0.1, 0.2, 0.6))
# look at the data
data## [1] 3 4 5 4 5 5 5 5 5 5 5 3 5 5 5 4 5 5 5 3 3 5 4 5 5 5 5 2 4 5 5 5 4 3 2 5 5 4 5 2 4 4 3 5 5 5 4 5 5 4# convert the vector to factor and control the levels and labels.
factor(x = data,
levels = c(1,2,3,4,5),
labels = c("rotten", "poor", "ok", "good", "excellent"))## [1] ok good excellent good excellent excellent excellent excellent excellent excellent excellent ok excellent excellent
## [15] excellent good excellent excellent excellent ok ok excellent good excellent excellent excellent excellent poor
## [29] good excellent excellent excellent good ok poor excellent excellent good excellent poor good good
## [43] ok excellent excellent excellent good excellent excellent good
## Levels: rotten poor ok good excellent## int [1:50] 3 4 5 4 5 5 5 5 5 5 ...You might have noticed that nobody rated “Cosmos” as “rotten”. But nonetheless, the levels argument allows us to specify what “could have been” scored. The labels are important for graphing, as we’ll see in later chapters.
Conversion between some data types is not possible. For example, we noted earlier that we can convert a number to character data, but the converse is not always true. If we try to store character data as numeric data R will not allow it, and will both warn us and then replace all invalid elements with NA values.
## [1] "dog" "10" "TRUE"# attempt to convert it to "numeric"; which elements do you think will be preserved?
mixed.num <- as.numeric(mixed)
# take a look how we did
mixed.num## [1] NA 10 NASo while R will convert “TRUE” to TRUE automatically when evaluating it as a logical, it will not convert “TRUE” to 1 with as.numeric().
As an aside, you might have noticed the name of the object mixed.num includes a period. This is fine, and many coders use a period to separate words in a name. You can also use and underscore if you prefer.
Exercise: Change the Data Types
- Coerce the vector c(1,1,0,1,0) to logical TRUE and FALSE values.
- Coerce the vector c(1,1,0,1,0) to character values.
- Create a vector of 10 values, filled with random numbers between 1 and 100.
- Add a random number between 0 and 1 to each value in your vector.
- Find your vector’s datatype.
- Coerce your vector’s datatype to integers.
This is a great time for a short coffee break.
Figure 4.6: Time to stretch.
4.4 Object Types
We’ve asked you to think of an object like a shoebox – a “thing” that can hold something. But shoeboxes come in different flavors: Nike shoeboxes hold running shoes, while The North Face shoeboxes hold hiking boots, and KEEN shoeboxes hold sandals (more or less). The same goes for objects in R.
There are five main object “classes” that hold different types of data:
1. Vectors
2. Matrices
3. Arrays
4. Lists
5. Dataframes
Actually, there are more than 5, but these are commonly used. The simplest way to give you an overview of these types is to use a spreadsheet analogy.
Figure 4.7: R objects in spreadsheet view.
A vector is a single row or column of data. The cells A1:A3 are highlighted, and you can see that this group of cells is named mixed (see the upper left of the figure). This particular vector has three elements within it, and it stores data that have a mode of character. Similarly, cells B1:B3 make up a vector called mixed2. Cells C1:C3 make up another vector (arbitrarily called numbers) that stores numeric datatypes. As we’ve already seen, vectors store only one datatype – they cannot store values with different datatypes.
Cells B1:C3 can be thought of as a matrix object. Matrices can store only a single datatype (usually numbers). Let’s suppose that these cells are called my.matrix. If we could make this matrix have many dimensions (like a cube of numbers), it would be called an array. Arrays can have multiple dimensions, but like matrices, can store only a single datatype. We’ll work with arrays extensively in Chapter 12.
In R, objects can be combined into a list. For example, in the spreadsheet example, we can combine mixed (a vector), mixed2 (a vector), and my.matrix (a matrix) into a new type object, a list. Lists are a very important concept in R. They are collections of objects, sort of like a shoe store – it can hold shoeboxes of all sorts, even other shoe stores! Many functions (like statistical functions) return the results in lists, where each portion of the list holds different kinds of information.
Finally, cells A1:C3 together can be thought of as a dataframe, which is a special type of list that is composed of many different vectors, all of the same length. In this example, our dataframe consists of the three vectors, mixed, mixed2, and numbers.
Each of these object types has unique properties, so we’ll work through them one by one. Keep in mind that we are aiming for the big picture here!
4.5 Vectors
We’ve already made several vectors in R – just look at your work in the Environment tab and look for the square brackets. Do you see the word vector anywhere? We don’t. That’s because a vector is the simplest type of object in R, and we suppose it is the default object type and not worth highlighting this fact in the environment’s grid view. When an object is a vector, the Type column displays the type of data held within the vector (its mode). If you want to verify whether an object is a vector, use the is.vector function, and pass to it the name of the object you wish to test; R will return either TRUE or FALSE depending on whether the object is a vector or not.
We’ve created vectors using the c function, the seq function, the sample function, and the runif function. Let’s create a new vector called my.vector that combines two of our previous vectors. Remember that vectors can store only a single datatype, so we’ll combine two vectors that contain numbers:
# use the c function to combine the two vectors, fiveIntegers and fiveRandoms into a new object called my.vector
my.vector <- c(fiveIntegers,fiveRandoms)
# look at the object
my.vector## [1] 60.0000000 2.0000000 45.0000000 20.0000000 99.0000000 0.8573828 0.3514372 0.1363997 0.4367107 0.1694715You can see that this is one long vector now stores a numeric datatype. The R output shows all 10 elements, but the display may require multiple lines of output to show them all. If so, keep in mind that the vectors indices can be identified by brackets. For example, the [1] in the first row of the output means the output begins with the first element of the vector, which is 60.
Now let’s return to our very first example in this primer:
## [1] 3.162278It should be clear now that the result, 3.162, is stored in a vector, and R is displaying the first element of this vector.
We can use the length function to find out how many “elements” our vector has:
## [1] 10Now we have a shoebox that is named my.vector, and it has a scrap of paper on it with 10 numbers (in a particular order). How do we open the shoebox to pull a particular number out? We use R’s indexing method for vectors, which are square brackets [ ].
Each of the 10 numbers (or elements) in my.vector has a position within the vector, and R has a specific syntax for pulling certain elements out of the vector object. Here are 7 examples:
- To get the first element stored in my.vector, use my.vector[1]
- To get the third element stored in my.vector, use my.vector[3]
- To get the first three elements stored in my.vector, use my.vector[1:3]
- To get elements 3, 5, 7, and 8, use my.vector[c(3,5,7,8)]
- To return everything but elements 1, 3, 7, and 8, use my.vector[-c(1,3,7,8)]
- To get all of the elements, except the fifth element, use my.vector[-5]
- To get the last three elements only, use my.vector[-(1:7)]
Remember that an index is a position within the vector. Since my.vector has 10 elements, the indices are 1 through 10. If we want to select certain indices from my.vector, we can simply identify the ones we want (see examples 1 through 4). Of these, example 4 is “tricky” because my.vector[c(3,5,7,8)] embeds a c function so that we can pull out various combinations of numbers, in the specified order. You’ll find this to be a very, very useful approach. You can’t just type in my.vector[3,5,7,8] because R will think you are trying to extract an element from a four dimensional array!
If we want to exclude certain indices, we use a - symbol, as shown in examples 5, 6, and 7. Example 6 is pretty straightforward: my.vector[-5] means return all elements of my.vector except the fifth element. But example 7 is tricky. The my.vector[-(1:7)] example uses parentheses to surround the numbers 1 through 7. If we didn’t have the parentheses, we would get an error. Try this:
Error in my.vector[-1:7] : only 0's may be mixed with negative subscriptsWhat the error says is an important troubleshooting message! There error says “only 0’s may be mixed with negative subscripts”. A negative subscript indicates exclusion, but -1 is mixed with 7. You can’t omit some indices and select others at the same time. By entering my.vector[-(1:7)], we are telling R to exclude indices 1 through 7.
Quick tip: In the RStudio editor, notice that when you type the opening square bracket [, the Editor automatically adds the closing square bracket. The Editor shows sets of parentheses in the same way. In addition, if the cursor is located immediately after either a parentheses or square bracket, the Editor highlights the corresponding syntax in the text. This is very useful because coding mistakes often occur when a parenthesis or bracket is out of place.
Exercise: Working with Vectors
- Create a vector (object) named “family” and enter the names of your (or a fictitious) family.
If you have a really small family, you can add some friends in there too. Don’t forget the quotes!
- Use the
lengthfunction to find the length of your vector. - Use the
strfunction to find the structure of this new object. - Use the
classfunction to find the class of the data within the object called “family”. - Extract the shortest family member.
- Extract the two oldest family members, and assign them to a new object called “elders”.
- Look at the object called “elders”.
- Extract the two oldest family members again, but this time reverse their order.
Assign them to a new object called “elders2”. - Look at the object called “elders2”.
We’ve been using the index number (or position within a vector) to refer to data within our vector. But it is also very useful to name the elements within a vector so that you can extract them by name instead of by index. Let’s do that now.
Suppose someone hands you a single shoebox that contains a pair of shoes. Its brand is Nike, the size is 10, and the model is “Pegasus”. We can create an object called shoebox that is a vector, and each element of the vector is named:
# create a new object called shoebox
shoebox <- c(brand = "Nike", size = 10, model = "Pegasus")
# look at the object called shoebox
shoebox## brand size model
## "Nike" "10" "Pegasus"By now you should see that the object called shoebox is storing data that are characters. See the quotes? Can you also see that each element is named? The names are also characters (though since they are being displayed as element names, they are not wrapped in quotes). The names are provided in the top row, and we can view them with the names function:
## [1] "brand" "size" "model"Our shoebox now has some attributes associated with it. From dictionary.com, we see that an attribute is “something attributed as belonging to a person, thing, group, etc.; a quality, character, characteristic, or property.”
Names are just one of many attributes an object can have. We will learn more about attributes later in this chapter.
When elements are named, we can extract by name instead of by index.
## brand
## "Nike"## brand
## "Nike"## size model
## "10" "Pegasus"## brand size model
## "Nike" "11" "Pegasus"
Exercise: Working with Named Vectors
- Think of one of your favorite animals. Create a vector with the name of that animal that contains three
elements that describe the animal. Name each element and provide a value.
- Use the
lengthfunction to find the length of your vector. - Use the
strfunction to find the structure of this new object. - Use the
classfunction to find the class of the data within the object you created. - Extract the first element by name.
- Extract the first and third elements by name.
- Teaser: add one more named element to your vector that describes something new about your animal.
4.6 Matrices
A matrix is a special case of a vector object with two dimensions that stores only one datatype (dimension is another example of an attribute). You can create a matrix easily with the matrix function.
First, let’s look at this function’s helpfile:
We can focus on the arguments for the matrix function using the args function:
## function (data = NA, nrow = 1, ncol = 1, byrow = FALSE, dimnames = NULL)
## NULLThis function has several arguments, including data, nrow, ncol. The default values are specified, so if you do not enter an argument, R will use the default values. For example, if you don’t provide the byrow argument, R will use FALSE.
Let’s create a matrix with 3 rows and 2 columns, and fill the matrix with random numbers (uniform random numbers between 0 and 1).
## [1] 0.5016476 0.7216185 0.2949530 0.1878342 0.9219681 0.1930997# create an object called my.matrix that is a matrix object
my.matrix <- matrix(data = numbers, nrow = 3, ncol = 2)
# look at the object, my.matrix
my.matrix## [,1] [,2]
## [1,] 0.5016476 0.1878342
## [2,] 0.7216185 0.9219681
## [3,] 0.2949530 0.1930997Because we did not provide the byrow argument, R used the default value, which is FALSE. This means we filled the matrix by column, which you can confirm directly. Since we used the default value of FALSE, R filled in the 6 elements of the matrix on a column-by-column basis. This means we snaked the vector that created the matrix first down column 1 and then down column 2.
What does the [,1] [,2] mean in the first row? That is the header of our matrix. Column 1 is identified as [,1], while column 2 is identified as [,2]. In this bracket notation, the rows are always identified first, followed by a comma, then followed by the column identifier. Remember this order: [Rows, Columns] . . . think of Russell Crowe or Ray Charles. This order might also be familiar if you’ve studied linear algebra. If an identifier is not specified but the comma placeholder is present, it means “all”. So [,1] means “all rows, column 1”, while [,2] means “all rows, column 2”.
The portions [1, ] [2, ] [3,] represent our row headers, where [1, ] means “row 1, all columns” and [2, ] means “row 2, all columns”, and [3, ] means “row 3, all columns”.
Now look for my.matrix in your Global Environment. You should see that the “Type” is listed as matrix. This is its class. You can also tell it is a matrix by looking in the Value column. See the notation [1:3, 1:2]. This notation tells you my.matrix is a 3 row by 2 column matrix, and the num that preceeds it tells you that it stores numeric values (its mode).
Figure 4.8: The grid view.
Obviously, we just created this matrix, but if we didn’t know much about it, we could use the nrow and ncol functions to get more information about this object.
## [1] 3## [1] 2The dim function is also useful for returning both answers at once, knowing that the number of rows is always given first, followed by the number of columns. Remember Russell Crowe?
## [1] 3 2What if we tried getting the number of columns for one of the vectors we made previously, say, mixed?
## NULLYou can see that R returns NULL. The reason is that we are using a function that is meant for objects that have multiple dimensions, and not one-dimensional vectors.
What about length?
## [1] 6Here’s another surprise, but this one is important. At its core, a matrix is a vector (with dimension attributes). The function length pertains to vectors, and since matrices are vectors with dimensional attributes, length returns the count of elements in the matrix. Think of a matrix as a vector that “snakes” around the rows and columns in a specified direction. For example, you can ask R to return all of the elements in the matrix using vector notation as follows:
## [1] 0.5016476 0.7216185 0.2949530 0.1878342 0.9219681 0.1930997Looks like a vector, right?
You can never go wrong by using the trusty str function; it will provide the dimensions. Just don’t get thrown off when you see that the values in your matrix are different from ours. Recall that they were generated randomly with the runif function!
## num [1:3, 1:2] 0.502 0.722 0.295 0.188 0.922 ...Here, the output [1:3, 1:2] suggests that the object type is a matrix. The first section 1:3 is for Rows, and the section 1:2 gives us the Column, separated by a comma. This suggests that to extract data out of this object, we will need to specify the row index and the column index, separated by a comma. We’ll refer to this matrix indexing throughout this primer. Let’s try it:
## [1] 0.9219681## [1] 0.5016476## [1] 0.7216185 0.9219681## [1] 0.5016476 0.7216185 0.2949530When you want to include all of the rows, or all of the columns from a matrix, as we did in the last two examples, just leave the index number off.
If we want to get all values in the first column but forget to add the comma placeholder, we end up with [1], which is vector indexing for the first element of the matrix.
## [1] 0.5016476Unless that is what you want, don’t forget the comma!
If the last two examples seem to be too vague (a blank space before or after a column), you could add in the built in names for rows and columns, like this:
## [1] 0.7216185 0.9219681## [1] 0.5016476 0.7216185 0.2949530Did you notice the argument called dimnames when you created your matrix? We omitted that argument too, but now let’s add it.
Go back to the matrix function helpfile, and review the example for creating a matrix. We’ll alter this helpfile example a tiny bit by adding in some additional argument names.
# from the matrix function helpfile: create a new object that is a matrix with the name mdat
mdat <- matrix(c(1,2,3, 11,12,13),
nrow = 2,
ncol = 3,
byrow = TRUE,
dimnames = list(c("row1", "row2"),
c("C.1", "C.2", "C.3")))
# same code but with rows and columns argument names included
mdat <- matrix(data = c(1,2,3, 11,12,13),
nrow = 2,
ncol = 3,
byrow = TRUE,
dimnames = list(rows = c("row1", "row2"),
columns = c("C.1", "C.2", "C.3")))Let’s work through this code, and use a visual aid to guide us:
Figure 4.9: Creating a matrix in R.
We use the matrix function to create a matrix with 2 rows and 3 columns. We will fill the 6 elements of the matrix with the numbers 1, 2, 3, 11, 12, 13. These will be filled by rows (so 1, 2, and 3 will occupy row 1; 11, 12, and 13 will occupy row 2). The dimnames argument will be used to name the rows and columns, and we’ll store the names in a list (the shoestore), which is what is required by the dimnames argument. Russell Crowe is telling us that we need to name the rows first, and we’ll use the c function to create a vector called “rows”, and pass in the elements “row1” and “row2”. We’ll use a second c function to create another vector called “columns” to name the columns “C.1”, “C.2”, and “C.3”. Notice that the names are stored in a list (a type of object), and that the actual row and column names must be character datatypes (in quotes). Let’s have a look at our newly created matrix:
## columns
## rows C.1 C.2 C.3
## row1 1 2 3
## row2 11 12 13Take a look at mdat in your environment, and carefully examine its type, length, size and value.
Figure 4.10: Creating a matrix in R.
Now we can use the names of the rows and columns to extract data from our object. Don’t forget that a comma must be supplied to separate the rows and columns, and don’t forget that names are characters that must be supplied with quotes!
## C.1 C.2 C.3
## 1 2 3## [1] 2Now let’s look at this object’s structure.
## num [1:2, 1:3] 1 11 2 12 3 13
## - attr(*, "dimnames")=List of 2
## ..$ rows : chr [1:2] "row1" "row2"
## ..$ columns: chr [1:3] "C.1" "C.2" "C.3"The output here is very revealing (good old str!). We see the word num which indicates that the data are numeric. We see [1:2, 1:3] which gives us the dimensions of the matrix. We then see the 6 elements that constitute the matrix.
We also see attr(*,“dimnames”)=List of 2. What on earth is this? When we created our matrix, we created an attribute for our object called dimnames. This attribute, in turn, is a list that contains two vectors (List of 2). Remember that a list is the shoestore…a list can hold vectors, arrays, matrices, and even other lists! This list holds two vectors. The first vector is called rows, which is a vector of characters with elements “row1” and “row2”. The second vector is called columns, which is a vector of characters with elements “C.1”, “C.2”, and “C.3”. Each part of the list begins with a dollar sign $.
We will talk about attributes and lists in a few minutes. (If you’re inclined, try re-running the code, but set the by.row argument to FALSE and see what happens!).
Exercise:
- Create a 3*2 matrix with random integers between 30 and 50.
- Name the rows Winken, Blinken, and Nod. Name the columns Height and Weight.
- Extract the height of Winken.
- Extract the weight of Nod.
- Find the average weight with the mean function.
4.7 Arrays
Array objects are very similar to matrices, except that they can have more than two dimensions. You can build an array with the array function.
## function (data = NA, dim = length(data), dimnames = NULL)
## NULLNotice that the argument names are very similar to the matrix function: data is the data you want to fill into the cells or elements, dim gives the dimensions, and dimnames lets you name the dimensions.
Let’s create an array called tauntauns, that tracks the number of individuals through 5 years, ages 0 through 10, and both sexes (male and female). We’ll fill this array with 0’s to begin with, and then will populate the array with random numbers. We’ll need 5 * 11 * 2 = 110 random numbers to fill the entire array. There are 11 age classes because we include 0 year olds.
# create an object called tauntauns that is an array
tauntauns <- array(data = 0,
dim = c(5,11,2),
dimnames = list(year = 1:5, age = 0:10 , sex = c("male", "female")))
# look at the object called tauntauns
tauntauns## , , sex = male
##
## age
## year 0 1 2 3 4 5 6 7 8 9 10
## 1 0 0 0 0 0 0 0 0 0 0 0
## 2 0 0 0 0 0 0 0 0 0 0 0
## 3 0 0 0 0 0 0 0 0 0 0 0
## 4 0 0 0 0 0 0 0 0 0 0 0
## 5 0 0 0 0 0 0 0 0 0 0 0
##
## , , sex = female
##
## age
## year 0 1 2 3 4 5 6 7 8 9 10
## 1 0 0 0 0 0 0 0 0 0 0 0
## 2 0 0 0 0 0 0 0 0 0 0 0
## 3 0 0 0 0 0 0 0 0 0 0 0
## 4 0 0 0 0 0 0 0 0 0 0 0
## 5 0 0 0 0 0 0 0 0 0 0 0When we look at this object, we can see that the years are given in the rows, which we specified as our first dimension, dim = c(5,11,2). The ages are given by the columns, which we specified as our second dimension, dim = c(5,11,2). Because we have a third dimension, this array is shown in two blocks, one for males and one for females. In total, there are 110 cells of data.
Look for the object called tauntauns in your Environment. Can you see that it’s type is listed as “array”?
Figure 4.11: The grid view.
Now let’s generate 110 random numbers between 100 and 500 with the help of the sample function. This will result in a new object called individuals, which is a vector containing numbers that represent the number of individuals of a given age and sex in a given year. Then, we’ll replace the 0’s in the tauntauns array with the numbers stored in individuals. The notation here is tauntauns[,,]. Can you see why? Just like the matrix had dimensions that were separated by commas, so too the array has dimensions separated by commas. Here, with no entries between the commas, it means “select all of the years, select all of the ages, and select both of the sexes, then fill them in with a random number between 100 and 500.” Make sure to look for the “snaking” route in this example.
# replace the 0's with random numbers between 100 and 500
individuals <- sample(x = c(100:500), size = 110)
# look at the individuals
individuals## [1] 398 135 348 211 420 199 119 113 170 252 128 205 154 118 404 410 386 476 351 104 377 274 125 184 491 460 210 226 317 356 496 412 421 293 469 255
## [37] 206 277 190 301 423 156 217 483 228 282 448 232 262 416 172 467 368 120 240 121 425 214 387 450 178 466 413 331 212 251 133 366 271 399 219 375
## [73] 244 394 173 288 447 108 160 367 369 462 259 364 127 185 152 481 192 382 285 424 134 222 391 436 157 102 435 328 475 493 488 419 459 428 115 175
## [109] 196 465# replace the array 0's with random numbers
tauntauns[,,] <- individuals
# look at the object called tauntauns
tauntauns## , , sex = male
##
## age
## year 0 1 2 3 4 5 6 7 8 9 10
## 1 398 199 128 410 377 460 496 255 423 282 172
## 2 135 119 205 386 274 210 412 206 156 448 467
## 3 348 113 154 476 125 226 421 277 217 232 368
## 4 211 170 118 351 184 317 293 190 483 262 120
## 5 420 252 404 104 491 356 469 301 228 416 240
##
## , , sex = female
##
## age
## year 0 1 2 3 4 5 6 7 8 9 10
## 1 121 178 251 219 288 369 185 285 436 475 428
## 2 425 466 133 375 447 462 152 424 157 493 115
## 3 214 413 366 244 108 259 481 134 102 488 175
## 4 387 331 271 394 160 364 192 222 435 419 196
## 5 450 212 399 173 367 127 382 391 328 459 465Let’s use the str function to look at the information associated with this object:
## num [1:5, 1:11, 1:2] 398 135 348 211 420 199 119 113 170 252 ...
## - attr(*, "dimnames")=List of 3
## ..$ year: chr [1:5] "1" "2" "3" "4" ...
## ..$ age : chr [1:11] "0" "1" "2" "3" ...
## ..$ sex : chr [1:2] "male" "female"The first section of this output, num [1:5, 1:11, 1:2] gives us the dimensions of our array, and tells us that the array is storing numbers. Once again, we see that our object called tauntauns has an attribute called “dimnames”. This attribute is a list with three sections (List of 3), and the sections are identified as year, age, and sex. Notice the dollar signs that identify each part, and that the names are all in quotes.
To extract information from the array, we need to specify all three dimensions. We can do this in a few different ways:
## age
## year 0 1 2 3 4 5 6 7 8 9 10
## 1 121 178 251 219 288 369 185 285 436 475 428
## 2 425 466 133 375 447 462 152 424 157 493 115
## 3 214 413 366 244 108 259 481 134 102 488 175
## 4 387 331 271 394 160 364 192 222 435 419 196
## 5 450 212 399 173 367 127 382 391 328 459 465# extract the female data for all years and all ages, but omit the names of the indices
tauntauns[, , 'female']## age
## year 0 1 2 3 4 5 6 7 8 9 10
## 1 121 178 251 219 288 369 185 285 436 475 428
## 2 425 466 133 375 447 462 152 424 157 493 115
## 3 214 413 366 244 108 259 481 134 102 488 175
## 4 387 331 271 394 160 364 192 222 435 419 196
## 5 450 212 399 173 367 127 382 391 328 459 465## sex
## age male female
## 0 348 214
## 1 113 413
## 2 154 366
## 3 476 244
## 4 125 108
## 5 226 259
## 6 421 481
## 7 277 134
## 8 217 102
## 9 232 488
## 10 368 175# extract the number of 2 year olds;
# notice that quotes are needed because "2" is a name
tauntauns[year = , age = "2", sex = ]## sex
## year male female
## 1 128 251
## 2 205 133
## 3 154 366
## 4 118 271
## 5 404 399# extract the 2nd index for age; watch the indexing here:
# 2 is the second index (which is "1" year olds), whereas "2" year olds are index 3
tauntauns[, 2, ]## sex
## year male female
## 1 199 178
## 2 119 466
## 3 113 413
## 4 170 331
## 5 252 212# extract the number of 1 and 3 year old males in year 3
tauntauns[year = 3,age = c("1","3"), sex = 'male']## 1 3
## 113 476## sex
## age male female
## 0 348 214
## 1 113 413
## 2 154 366
## 3 476 244
## 4 125 108
## 5 226 259
## 6 421 481
## 7 277 134
## 8 217 102
## 9 232 488
## 10 368 175## sex
## age male female
## 0 348 214
## 1 113 413
## 2 154 366
## 3 476 244
## 4 125 108
## 5 226 259
## 6 421 481
## 7 277 134
## 8 217 102
## 9 232 488
## 10 368 175## sex
## year male female
## 1 128 251
## 2 205 133
## 3 154 366
## 4 118 271
## 5 404 399Double check your work to make sure you’re getting the result you should! You must know (and understand) the order of the array’s dimensions. And you must always be careful to use quotes when selecting data based upon a dimensional attribute as opposed to selecting data based on the index. Again, the str function can come to the rescue.
Exercise: Extracting from an Array
Extract the following pieces of information from the object, tauntauns:
- Extract age 10
- Extract males of age 10
- Extract males of age 10 in year 4
- Extract females of ages 1:3
- Change the number of males, age 2, year 5 to 100
- Find the total population size in year 5
- Find the total male population size in year 2
- Extract age 4 males in year 3 by index.
- Extract age 4 males in year 3 by name.
R has another type of object called a table, which is an array of integer values. Objects of class table can be created from, of all things, the table function, which builds contingency tables for factor datatypes. We’ll see tables in use in future chapters.
4.8 Lists
We’ve briefly touched on lists, and you’ve already created some lists when you named your matrix and array dimensions. Now let’s look at lists in more detail. If objects are shoeboxes, lists are grocery carts. A list is, well, a list or collection of different objects. The objects can be vectors, matrices, arrays, or even other lists. The main thing to know about lists is that they are “layered” or hierarchical, so to add new objects to a list, or to extract objects from a list, you need to specify even more information than when you extract information from an matrix or array.
Let’s create a list (using the list function) called my.list that is a combination of the objects fiveIntegers, today, and mdat:
Look for the new object, my.list, in your Environment, and you’ll see that this list holds three objects.
Figure 4.12: my.list is a list of 3 objects.
Do you see a magnifying glass to the right of the Value column? Click on that
Figure 4.13: Use the magnifier to inspect the list.
Now let’s take a look at your object, my.list, with code:
## [[1]]
## [1] 60 2 45 20 99
##
## [[2]]
## columns
## rows C.1 C.2 C.3
## row1 1 2 3
## row2 11 12 13
##
## [[3]]
## [1] "Wed Feb 10 10:13:16 2021"This looks a bit ugly, but look for the double brackets [[ ]] . When you see double brackets, you know you are working with a list. You already know that our list has three parts to it. Can you see [[1]], [[2]], and [[3]]? These identify the objects that make up the list: [[1]] is the vector fiveIntegers, [[2]] is the matrix mdat, and [[3]] is the vector today. We didn’t name the sections of this list, so the indices are numbered.
To extract information from a list, first you must point to the index in the highest level of the list with the double brackets:
## [1] 60 2 45 20 99## [1] "Wed Feb 10 10:13:16 2021"Note that the double bracket notation will extract the list element, and return its original class:
## [1] "character"Alternatively, if you want to return a list, use the single bracket extractor on a list object:
## [1] "list"List indexing can be confusing, but it can be conquered with practice. If you want to extract the first integer in fiveIntegers, you would need to first point to extract the section of the my.list that contains the object fiveIntegers (a vector), and then do the subsetting of fiveIntegers, like this:
## [1] 60Note that if you were to extract a subset of data from the second object in the list (which is a matrix), you would need to use matrix notation (good old Russell Crowe again). For example:
## row1 row2
## 1 11If you named the elements of your list, you can extract its pieces with the $ notation, which is equivalent to [[]].
# create a list object called my.list
my.list <- list("integers" = fiveIntegers, "matrix" = mdat, "today" = today)
# look at the structure of my.list
str(my.list)## List of 3
## $ integers: int [1:5] 60 2 45 20 99
## $ matrix : num [1:2, 1:3] 1 11 2 12 3 13
## ..- attr(*, "dimnames")=List of 2
## .. ..$ rows : chr [1:2] "row1" "row2"
## .. ..$ columns: chr [1:3] "C.1" "C.2" "C.3"
## $ today : chr "Wed Feb 10 10:13:16 2021"Here, you see the list but the objects are identified like this: $ integers:, $ matrix:, and $ today:. The dollar sign precedes the name of each section, and you can use this method to extract portions of your list, like this:
## [1] 60 2 45 20 99You can also use this method:
# we can extract the section named "integers" by referencing in the two square brackets
my.list[['integers']]## [1] 60 2 45 20 99The dollar sign separates the name of the list (my.list) and the element in the list that you want (integers). We will get a lot of practice using lists in future chapters.
Exercise:
- Create a list of 4 objects that are in your global environment.
- Name the sections of your list.
- Extract the first element of the list (the entire object).
- Extract from this list the first element WITHIN the first object in your list.
4.9 Data frames
The last object type that we’ll mention is a data frame, which is a list of vectors that all have the same length. Most datasets are stored as data frames in R, and we’ll get a lot of practice using them in the following chapters. For now, though, let’s combine the three vectors, fiveIntegers, fiveBooleans, and fiveRandoms into a data frame with the data.frame function. Let’s take a look at the help file:
Data frames are lists of vectors, but the vectors themselves can be different data types. (We already know that, within a vector, there can be only one data type, or mode).
# create a dataframe called my.data
my.data <- data.frame(fiveIntegers, fiveBooleans, fiveRandoms)
# look at the data
my.data## fiveIntegers fiveBooleans fiveRandoms
## 1 60 TRUE 0.8573828
## 2 2 FALSE 0.3514372
## 3 45 FALSE 0.1363997
## 4 20 FALSE 0.4367107
## 5 99 FALSE 0.1694715Now let’s use the rownames and colnames functions, which do what their name implies:
## [1] "fiveIntegers" "fiveBooleans" "fiveRandoms"## [1] "1" "2" "3" "4" "5"Data frames have row names and column names that are characters. You can see that data frames are two dimensional, so to extract information from them, you must specify both the rows and columns. Let’s use the trusty str function to get more information about this new object:
## 'data.frame': 5 obs. of 3 variables:
## $ fiveIntegers: int 60 2 45 20 99
## $ fiveBooleans: logi TRUE FALSE FALSE FALSE FALSE
## $ fiveRandoms : num 0.857 0.351 0.136 0.437 0.169The output is telling us that this data frame has 5 observations (rows) with 3 variables (columns). It then walks us through each column, in order, providing the data type of each column and the first few records within the column.
We won’t say more about data frames here because you’ll soon be working with them extensively.
4.10 Changing an Object’s Class
By now you know that R has a number of object classes, and you have practiced creating objects of various sorts. There may be times when we need a specific object type for the task at hand. For those times, R has coercion functions, which are generally used to convert an existing object to a new type as opposed to creating an entirely new object from scratch. We’ve seen a number of coercion functions that change datatypes (modes); recall that the coercion functions start with “as.” and end with the output class. Here are a few that convert objects from one type to another:
as.data.frame- converts an object to a data frameas.list- converts an object to a listas.matrix- converts an object to a matrixas.vector- converts an object to a vectoras.array- converts an object to an array
To see the coercion functions available to you, type as. into your console and press tab key once. Depending on what packages you have loaded, you may see 125 or more coercion functions! Most of them are not meant to be called by the user (you!), but are called by a core function behind the scenes.
Let’s revisit some of the objects we made earlier. Let’s convert my.matrix to a dataframe:
## [,1] [,2]
## [1,] 0.5016476 0.1878342
## [2,] 0.7216185 0.9219681
## [3,] 0.2949530 0.1930997## num [1:3, 1:2] 0.502 0.722 0.295 0.188 0.922 ...# convert my.matrix to a dataframe
my.matrix <- as.data.frame(my.matrix)
# look at the structure of my.matrix
str(my.matrix)## 'data.frame': 3 obs. of 2 variables:
## $ V1: num 0.502 0.722 0.295
## $ V2: num 0.188 0.922 0.193This worked out fine (assuming that a dataframe is what you want!). Also note how R named the rows and columns for you:
## V1 V2
## 1 0.5016476 0.1878342
## 2 0.7216185 0.9219681
## 3 0.2949530 0.1930997When row and column names are not provided by you, R will name each row of a new with dataframe numerical characters (i.e. 1, 2, 3, etc.), and name each column as V1, V2, V3, etc… (in reference to the fact that in dataframes, columns are typically the Variables of our data).
There are cases, however, where certain objects cannot be coerced to another. Let’s change our vector fiveIntegers to a dataframe, and then try to turn it back into a vector:
# turn the vector fiveIntegers into a dataframe
fiveIntegers <- as.data.frame(fiveIntegers)
# look at the structure of fiveIntegers
str(fiveIntegers)## 'data.frame': 5 obs. of 1 variable:
## $ fiveIntegers: int 60 2 45 20 99# now try to change it back to a vector
fiveIntegers <- as.vector(fiveIntegers)
# still a dataframe!
str(fiveIntegers)## 'data.frame': 5 obs. of 1 variable:
## $ fiveIntegers: int 60 2 45 20 99# convert the dataframe to a matrix
fiveIntegers <- as.matrix(fiveIntegers)
# look at the structure, note that it is a matrix
str(fiveIntegers)## int [1:5, 1] 60 2 45 20 99
## - attr(*, "dimnames")=List of 2
## ..$ : NULL
## ..$ : chr "fiveIntegers"# now convert from matrix to vector
fiveIntegers <- as.vector(fiveIntegers)
# look at the structure, note that it is a vector
str(fiveIntegers)## int [1:5] 60 2 45 20 99
Exercise: Change the Object Types
- Create a 3 by 3 matrix filled with random numbers between 1 and 100
- Coerce your matrix to a data frame
- Coerce your new data frame back to a matrix
- Create a new vector consisting of 10 elements
- Create a new list that contains your matrix and your vector
- Coerce the tauntauns: sex=“female” array to a matrix
4.11 S3 versus S4 Objects
We’ve been talking about objects as shoeboxes (e.g., you created an object called fiveNumbers which contains five integers. By now you know that different objects store different types of information. This metaphor works, generally, but we can take it one step further. All of the objects we have discussed so far are called S3 objects. Think of these objects as cardboard shoeboxes in that they are flexible with respect to the functions that operate on them. For instance, the function called print is actually a generic function that first finds out what class of object is to be printed, then calls the appropriate function for printing. For example, print.factor will print objects that are factors, while print.table will print objects that are tables. With S3 objects, you can use the generic function and R will dispatch the appropriate function.
Another class of objects are called S4 objects, which are usually list-like. They are inflexible and require specific functions to work on them. If a list can be thought of as a shopping cart filled with various objects, an S4 object is very rigid shopping cart. You can’t just throw in any old object anywhere in the cart – each part of the S4 cart holds specific information in the form of specific objects. We won’t delve into S3 vs S4 objects too much here, but we will create some S4 objects in chapter 6 and explore their properties with the str function.
4.12 Attributes
Before we end this chapter, it’s worth delving into the concept of attributes a bit more. Objects, whether they are arrays, matrices, data frames, vectors, or lists, have attributes. These attributes appear when you use the str function. We’ve already created an attribute for some objects called dimnames. But you can also add as many attributes to an object as you’d like. Here’s an excerpt from the R website:
“All objects except NULL can have one or more attributes attached to them. Attributes are stored as a pairlist where all elements are named, but should be thought of as a set of name = value pairs. A listing of the attributes can be obtained using attributes and set by attributes <-, individual components are accessed using attr and attr <-.”
Besides str, you can use the attributes function to list all of an object’s attributes. Let’s take a look at the array object we created called ‘tauntauns’:
## $dim
## [1] 5 11 2
##
## $dimnames
## $dimnames$year
## [1] "1" "2" "3" "4" "5"
##
## $dimnames$age
## [1] "0" "1" "2" "3" "4" "5" "6" "7" "8" "9" "10"
##
## $dimnames$sex
## [1] "male" "female"## num [1:5, 1:11, 1:2] 398 135 348 211 420 199 119 113 170 252 ...
## - attr(*, "dimnames")=List of 3
## ..$ year: chr [1:5] "1" "2" "3" "4" ...
## ..$ age : chr [1:11] "0" "1" "2" "3" ...
## ..$ sex : chr [1:2] "male" "female"A second function you should know about is the attr function. It can be used to retrieve specific attributes of an object:
## $year
## [1] "1" "2" "3" "4" "5"
##
## $age
## [1] "0" "1" "2" "3" "4" "5" "6" "7" "8" "9" "10"
##
## $sex
## [1] "male" "female"This same function can be used to create new attributes:
attr(x = tauntauns, which = "comment" ) <- "This is my tauntaun population array"
attr(x = tauntauns, which = "created.by") <- "Created by me"This comes in handy for large objects that you create that require metadata, or information about the object, that is connected to the object itself. Note that for many types of objects, attributes will not be shown when you call the object. Rather, you need to use the attributes function to view them. However, for arrays, attributes will be displayed just by calling the object.
4.13 Summary and A Little Pep Talk
That was a whirlwind tour of objects in R. We’ve talked about various datatypes, including numeric, integer, character, logical, factor, and date modes. We’ve also reviewed five main object “classes” that hold different kinds of data:
- Vectors - one dimensional series of elements that are all of the same mode.
- Matrices - two dimensional series of elements that are all of the same mode.
- Arrays - multi-dimensional series of elements that are all of the same mode.
- Lists - groups or bundles of different objects.
- Dataframes - a special kind of list which is composed of a series of vectors, each of the same length.
There are a few other kinds of objects as well, but these are the main classes that we’ll work with in this primer. It can be overwhelming to remember the different datatypes, the different object types, and the different functions that can be used for each. But you’ll make rapid progress if you keep these points in mind:
- When you create an object, always look in your Environment and see what is there.
- If you need to remember ONLY one function when it comes to objects, keep
strin your back pocket. It returns the datatype, the object type, and lists all of the object’s attributes. - For functions, the
helpfunction can never be overused. - Objects have attributes, and the
attrandattributesfunctions can be extremely helpful.
It may also be useful to peak at some of the following cheatsheets, and post those of interest by your computer:
In the next set of chapters, we’ll put on our Tauntaun biologist hats, and begin using R for data analysis and report writing. Onward!
4.14 Answers to Exercise
Always remember that in R, there are several ways to skin a cat. You may have arrived at different solutions to the exercises, and that’s fine! Below, we give examples of how the exercises could have been coded.
Exercise: Change the Datatypes
- Coerce the vector c(1,1,0,1,0) to logical TRUE and FALSE values.
- Coerce the vector c(1,1,0,1,0) to character values.
- Create a vector of 10 values, filled with random numbers between 1 and 100.
- Add a random number between 0 and 1 to each value in your vector.
- Find your vector’s datatype.
- Coerce your vector’s datatype to integers.
## num [1:5] 1 1 0 1 0# coerce to logical
my.vector2 <- as.logical(my.vector)
# Coerce the vector c(1,1,0,1,0) to character values
my.vector3 <- as.character(my.vector)
# Create a vector of 10 values, filled with random numbers between 1 and 100.
my.vector4 <- sample(x = 1:100, size = 10,replace = T)
#Add a random number between 0 and 1 to each value in your vector.
randoms <- runif(n = 10)
my.vector5 <- my.vector4 + randoms
# Find you vector's datatype.
class(my.vector5)## [1] "numeric"
Exercise: Working with Vectors
- Create a vector (object) named “family” and enter the names of your (or a fictitious) family.
If you have a really small family, you can add some friends in there too. Don’t forget the quotes!
- Use the
lengthfunction to find the length of your vector. - Use the
strfunction to find the structure of this new object. - Use the
classfunction to find the class of the data within the object called “family”. - Extract the shortest family member.
- Extract the two oldest family members, and assign them to a new object called “elders”.
- Look at the object called “elders”.
- Extract the two oldest family members again, but this time reverse their order.
Assign them to a new object called “elders2”. - Look at the object called “elders2”.
# Create a vector (object) named "family" and enter the names of your (or a fictitious) family
family <- c("Gilligan", "Skipper", "MaryAnn", "Professor", "Ginger", "Lovey", "Thurston")
# Use the `length` function to find the length of your vector
length(family)## [1] 7## chr [1:7] "Gilligan" "Skipper" "MaryAnn" "Professor" "Ginger" "Lovey" "Thurston"# Use the `class` function to find the class of the data within the object called "family".
class(family)## [1] "character"## [1] "Gilligan"# Extract the two oldest family members, and assign them to a new object called "elders".
elders <- family[6:7]
elders## [1] "Lovey" "Thurston"# Extract the two oldest family members again, but this time reverse their order.
elders2 <- family[7:6]
# Look at the object called "elders2".
elders2## [1] "Thurston" "Lovey"
Exercise: Working with Named Vectors
- Think of one of your favorite animals. Create a vector with the name of that animal that contains three
elements that describe the animal. Name each element and provide a value.
- Use the
lengthfunction to find the length of your vector. - Use the
strfunction to find the structure of this new object. - Use the
classfunction to find the class of the data within the object you created. - Extract the first element by name.
- Extract the first and third elements by name.
- Teaser: add one more named element to your vector that describes something new about your animal.
# Think of one of your favorite animals. Create a vector with the name of that animal that contains
# three elements that describe the animal. Name each element and provide a value.
leatherback.turtle <- c(diet="jellyfish", clutches = 7, clutch.size = 80)
# Use the `length` function to find the length of your vector
length(leatherback.turtle)## [1] 3# Use the `str` function to find the structure of this new object; note our example forces all
# elements to be characters
str(leatherback.turtle)## Named chr [1:3] "jellyfish" "7" "80"
## - attr(*, "names")= chr [1:3] "diet" "clutches" "clutch.size"# Use the `class` function to find the class of the data within the object you created.
class(leatherback.turtle)## [1] "character"## diet
## "jellyfish"## diet clutch.size
## "jellyfish" "80"# Teaser: add one more named element to your vector that describes something new about your animal.
leatherback.turtle["status"] <- "endangered"
leatherback.turtle## diet clutches clutch.size status
## "jellyfish" "7" "80" "endangered"
Exercise:
- Create an 3 by 2 matrix with random integers between 30 and 50.
- Name the rows Winken, Blinken, and Nod. Name the columns Height and Weight.
- Extract the height of Winken.
- Extract the weight of Nod.
- Find the average weight with the mean function.
# Create an 3 by 2 matrix with random integers between 30 and 50.
numbers <- sample(x = 30:50, size = 3 * 2, replace = T)
new.matrix <- matrix(data = numbers,nrow = 3, ncol = 2, byrow = T)
# Name the rows Winken, Blinken, and Nod. Name the columns Height and Weight.
dimnames(new.matrix) <- list(rows = c("Winken", "Blinken", "Nod"), cols = c("Height", "Weight"))
new.matrix## cols
## rows Height Weight
## Winken 47 32
## Blinken 50 35
## Nod 39 45## [1] 47## [1] 45## [1] 37.33333
Exercise: Extracting from an Array
Extract the following pieces of information from the object, tauntauns:
- Extract age 10
- Extract males of age 10
- Extract males of age 10 in year 4
- Extract females of ages 1:3
- Change the number of males, age 2, year 5 to 100
- Find the total population size in year 5
- Find the total male population size in year 2
- Extract age 4 males in year 3 by index.
- Extract age 4 males in year 3 by name.
## num [1:5, 1:11, 1:2] 398 135 348 211 420 199 119 113 170 252 ...
## - attr(*, "dimnames")=List of 3
## ..$ year: chr [1:5] "1" "2" "3" "4" ...
## ..$ age : chr [1:11] "0" "1" "2" "3" ...
## ..$ sex : chr [1:2] "male" "female"
## - attr(*, "comment")= chr "This is my tauntaun population array"
## - attr(*, "created.by")= chr "Created by me"# look at the tauntauns array so we can verify answers. But recall that since we
# generated these as random values using the sample function, your answers will differ from ours.
tauntauns## , , sex = male
##
## age
## year 0 1 2 3 4 5 6 7 8 9 10
## 1 398 199 128 410 377 460 496 255 423 282 172
## 2 135 119 205 386 274 210 412 206 156 448 467
## 3 348 113 154 476 125 226 421 277 217 232 368
## 4 211 170 118 351 184 317 293 190 483 262 120
## 5 420 252 404 104 491 356 469 301 228 416 240
##
## , , sex = female
##
## age
## year 0 1 2 3 4 5 6 7 8 9 10
## 1 121 178 251 219 288 369 185 285 436 475 428
## 2 425 466 133 375 447 462 152 424 157 493 115
## 3 214 413 366 244 108 259 481 134 102 488 175
## 4 387 331 271 394 160 364 192 222 435 419 196
## 5 450 212 399 173 367 127 382 391 328 459 465
##
## attr(,"created.by")
## [1] "Created by me"## sex
## year male female
## 1 172 428
## 2 467 115
## 3 368 175
## 4 120 196
## 5 240 465## 1 2 3 4 5
## 172 467 368 120 240## [1] 120## age
## year 1 2 3
## 1 178 251 219
## 2 466 133 375
## 3 413 366 244
## 4 331 271 394
## 5 212 399 173# Change the number of males, age 2, year 5 to 100
tauntauns["5", "2", "male"] <- 100
# Find the total population size in year 5
year.5 <- sum(tauntauns["5", , ])
year.5## [1] 7130# Find the total male population size in year 2
male.2 <- sum(tauntauns["2", , "male"])
# Extract age 4 males in year 3 by index
tauntauns[3, 5, 1]## [1] 125## [1] 125
Exercise:
- Create a list of 4 objects that are in your global environment.
- Name the sections of your list.
- Extract the first element of the list (the entire object).
- Extract from this list the first element WITHIN the first object in your list.
# Create a list of 4 objects that are in your global environment.
new.list <- list(letters, eleanor, birthday2, mixed)
# Name the sections of your list.
names(new.list) <- c("letters", "eleanor", "birthday", "mixed")
new.list## $letters
## [1] "a" "b" "c" "d" "e" "f" "g" "h" "i" "j" "k" "l" "m" "n" "o" "p" "q" "r" "s" "t" "u" "v" "w" "x" "y" "z"
##
## $eleanor
## [1] -31127
##
## $birthday
## [1] "1918-07-18"
##
## $mixed
## [1] "dog" "10" "TRUE"## [1] "a" "b" "c" "d" "e" "f" "g" "h" "i" "j" "k" "l" "m" "n" "o" "p" "q" "r" "s" "t" "u" "v" "w" "x" "y" "z"## [1] "a"