Ripple-carry Adder
With an understanding of basic logic gates, we can construct circuits that perform calculations like addition, multiplication, subtraction, and division.
Here we’ll construct an adder, specifically a 4-bit ripple-carry adder.
Our construction begins with a half adder. This takes two binary digits as operands (here A and B), and it produces the sum with XOR, and the carry with AND.
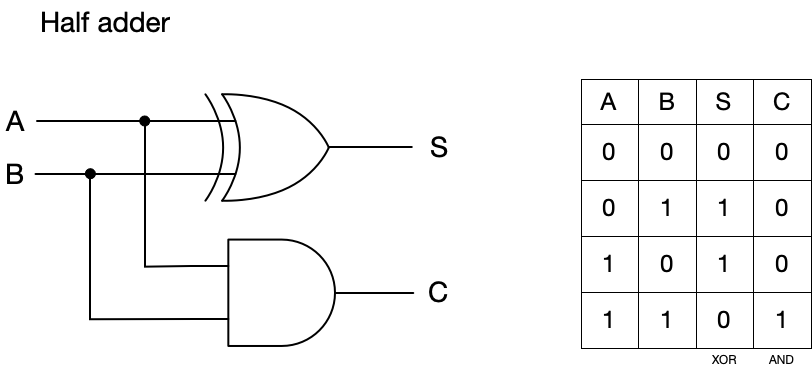
This works fine for one-bit addition, but it doesn’t support carry in, so it cannot be used as-is.
Combining two half adders and an additional OR gate we can construct a full adder. A full adder supports carry in, and can be used in our construction.
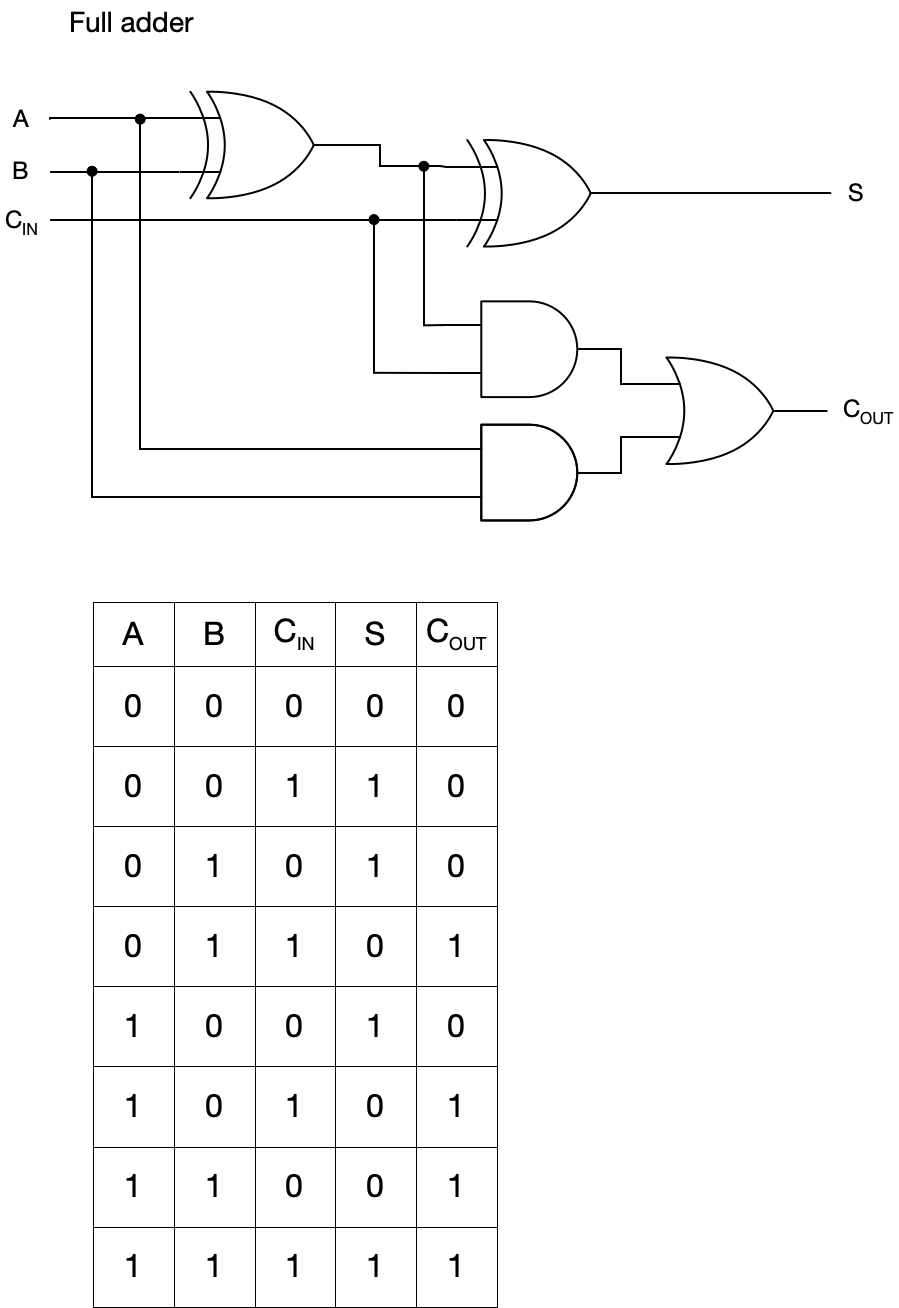
Notice that a full adder has three inputs, A, B, and carry in (C_{IN}), and two outputs, sum (S) and carry out (C_{OUT}). While a single full adder only operates on one-bit inputs, because full adders have both carry in and carry out multiple full adders can be chained together to construct multi-bit adders.
Here’s an example of a 4-bit ripple-carry adder constructed from four full adders.
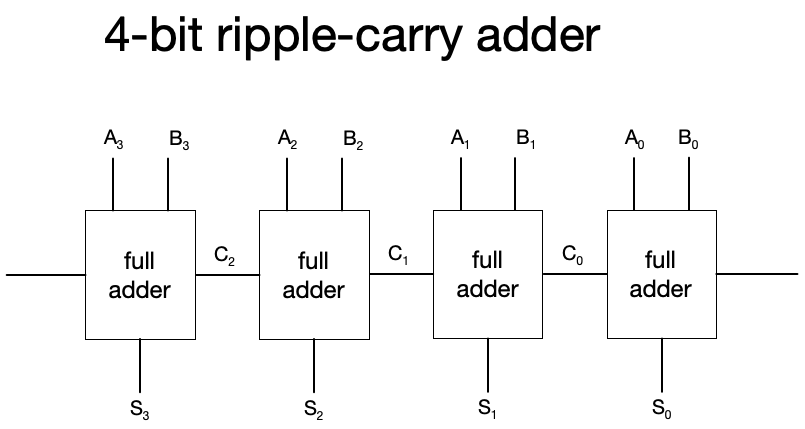
We need to interface individual bits of our operands and solution to complete the construction.
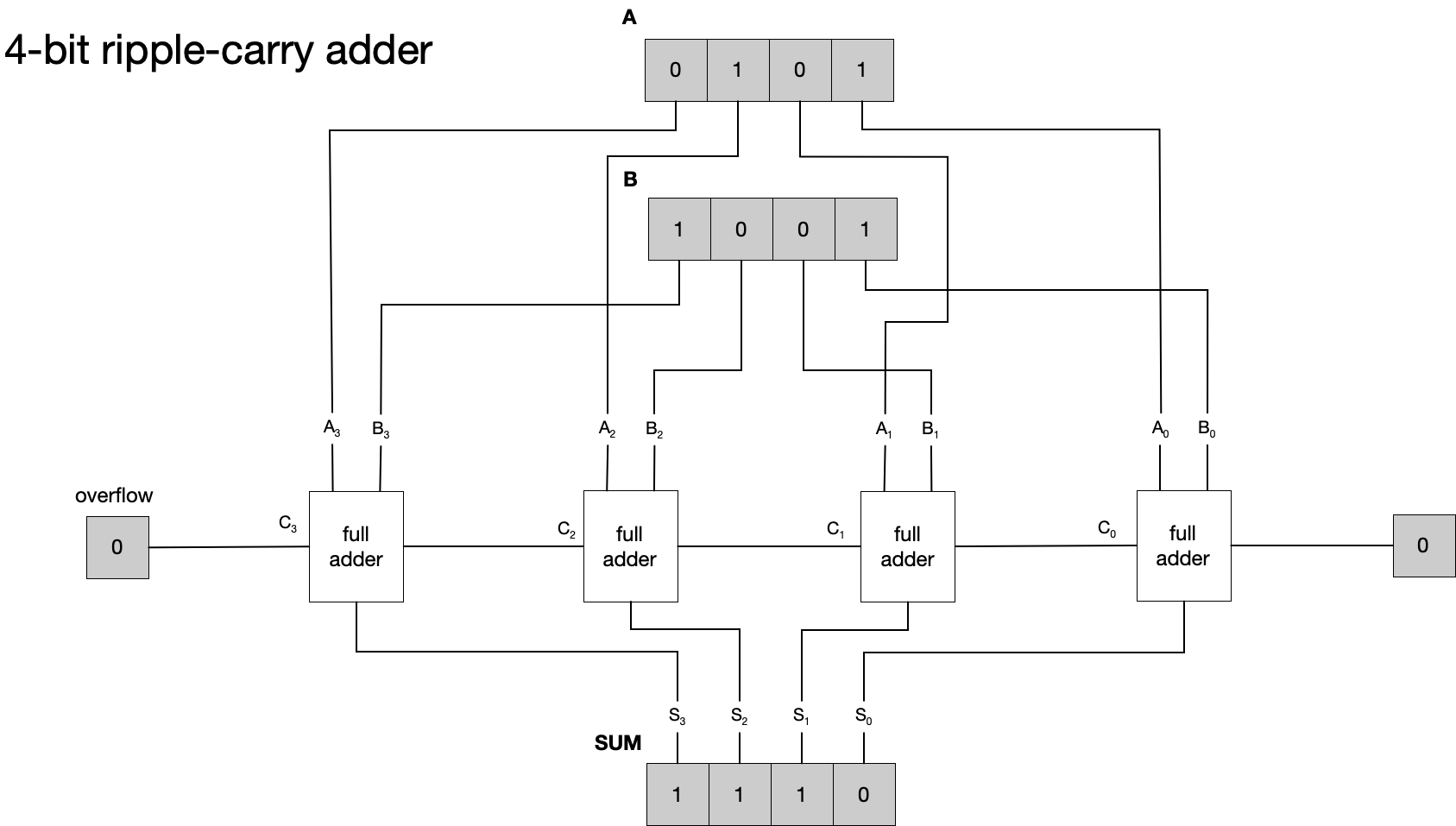
In this construction, each bit of the two operands is interfaced to the full adder for the corresponding power of two. While we could use a half adder for the lowest order bits (the 2^0 bits), here we’ve used a full adder with carry in of zero. The leftmost full adder adds bits A_0 and B_0. The sum goes to the lowest order bit in the result, and the carry out is propagated to the carry in of the next full adder to the left. So the next full adder to the left receives bits A_1 and B_1 as operands, and the carry in, and computes the sum and carry for the 2^1 bit. This proceeds in similar fashion to compute the two higher order bits. In the end, any carry out is held in the flag field labeled “overflow” and the sum of the operands A and B is left in SUM.
If we wanted to produce an 8-bit, 16-bit, 32-bit or any other larger adder, we could extend the construction to include more single-bit full adders.
If we wanted to simplify the circuit a little we could replace the first (rightmost) full adder with a half adder, and eliminate the need for constant 0 on the first carry-in (but we’ll see why we don’t do this later).
© 2025 Clayton Cafiero.
No generative AI was used in writing this material. This was written the old-fashioned way.