A binary puzzle, demystified

Author
Affiliation

Clayton Cafiero

University of Vermont

Published

2025-09-07

Let’s take a look at the cards again.

 

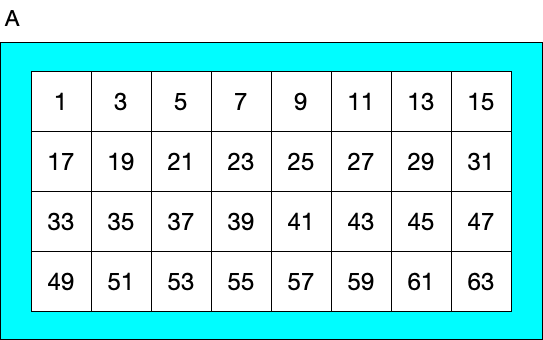
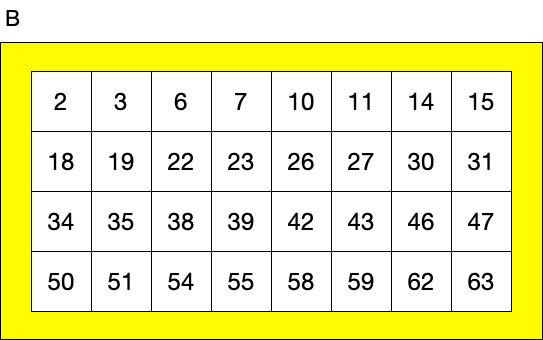
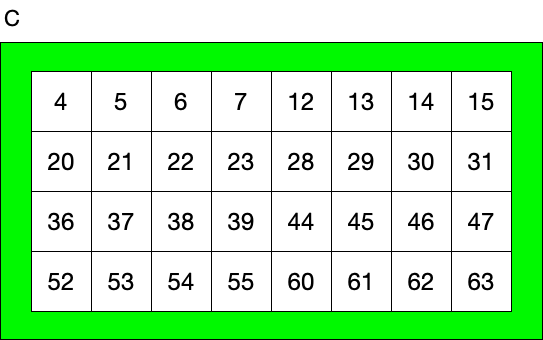
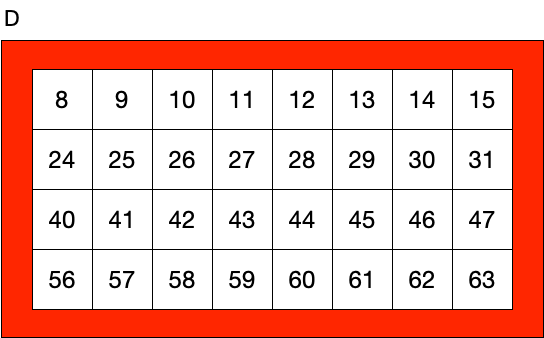
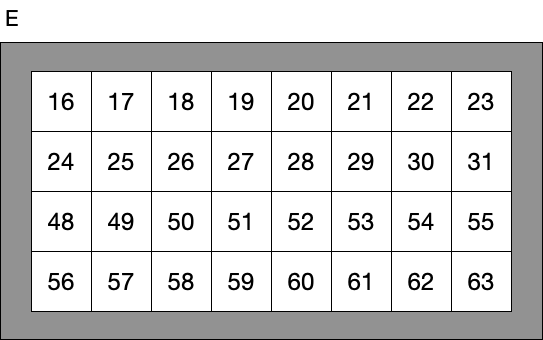
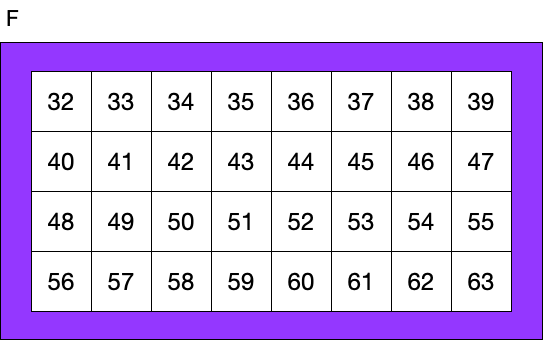
Clearly the numbers range from one to 63, and each card has exactly 32 numbers on it.

But how are the numbers organized? Why, for example, is 55 on cards A, B, C, E, and F, but not on card D? Why, for example, is 9 only on cards A and D?

Consider the binary representation of numbers from one to 63.

dec bin dec bin dec bin dec bin
16 010000 32 100000 48 110000
1 000001 17 010001 33 100001 49 110001
2 000010 18 010010 34 100010 50 110010
3 000011 19 010011 35 100011 51 110011
4 000100 20 010100 36 100100 52 110100
5 000101 21 010101 37 100101 53 110101
6 000110 22 010110 38 100110 54 110110
7 000111 23 010111 39 100111 55 110111
8 001000 24 011000 40 101000 56 111000
9 001001 25 011001 41 101001 57 111001
10 001010 26 011010 42 101010 58 111010
11 001011 27 011011 43 101011 59 111011
12 001100 28 011100 44 101100 60 111100
13 001101 29 011101 45 101101 61 111101
14 001110 30 011110 46 101110 62 111110
15 001111 31 011111 47 101111 63 111111

 

Now let’s focus on the numbers that appear on card A.

dec bin     dec bin     dec bin     dec bin
16 010000 32 100000 48 110000
1 000001 17 010001 33 100001 49 110001
2 000010 18 010010 34 100010 50 110010
3 000011 19 010011 35 100011 51 110011
4 000100 20 010100 36 100100 52 110100
5 000101 21 010101 37 100101 53 110101
6 000110 22 010110 38 100110 54 110110
7 000111 23 010111 39 100111 55 110111
8 001000 24 011000 40 101000 56 111000
9 001001 25 011001 41 101001 57 111001
10 001010 26 011010 42 101010 58 111010
11 001011 27 011011 43 101011 59 111011
12 001100 28 011100 44 101100 60 111100
13 001101 29 011101 45 101101 61 111101
14 001110 30 011110 46 101110 62 111110
15 001111 31 011111 47 101111 63 111111

 

What do you notice about the highlighted numbers? They’re all odd. How can you tell an odd number in binary? Easy. Just look at the least significant digit—that’s the ones column. If the digit is a 1, then the number is odd. Otherwise the number is even.

So we could say that card A includes all the odd numbers, but for sake of finding the general pattern, let’s say instead that _card A include all the numbers whose binary representation has a 1 in the 2^0 (ones) position.

Now you can probably guess how card B is populated, but look carefully, it’s not just even numbers. Give this a little more thought.

dec bin     dec bin     dec bin     dec bin
16 010000 32 100000 48 110000
1 000001 17 010001 33 100001 49 110001
2 000010 18 010010 34 100010 50 110010
3 000011 19 010011 35 100011 51 110011
4 000100 20 010100 36 100100 52 110100
5 000101 21 010101 37 100101 53 110101
6 000110 22 010110 38 100110 54 110110
7 000111 23 010111 39 100111 55 110111
8 001000 24 011000 40 101000 56 111000
9 001001 25 011001 41 101001 57 111001
10 001010 26 011010 42 101010 58 111010
11 001011 27 011011 43 101011 59 111011
12 001100 28 011100 44 101100 60 111100
13 001101 29 011101 45 101101 61 111101
14 001110 30 011110 46 101110 62 111110
15 001111 31 011111 47 101111 63 111111

 

These are all the numbers that have a 1 in the 2^1 column—the twos column. These are all the numbers on card B.

Here’s a table indicating which cards only contain numbers with a 1 in the indicated (binary) position.

card 2^5 (32) 2^4 (16) 2^3 (8) 2^2 (4) 2^1 (2) 2^0 (1)
A ✓
B ✓
C ✓
D ✓
E ✓
F ✓

 

So, 55 (binary 110111) appears on all the cards but D, because it has 1s in all the columns except the 2^3, 9 (binary 001001) appears only on cards A and D, because its binary representation has 1s only in the 2^0 column and the 2^3 column, and good old 42 appears on cards B, D and F because its binary representation (101010) has 1s only in the 2^1, 2^3, and 2^5 columns. The point is that the cards on which a number appears uniquely specifies those columns which have a one. If you know what cards a number appears on, you can uniquely determine the number.

Notice that the upper left-hand number on each card is a power of two.

card number
A 1
B 2
C 4
D 8
E 16
F 32

 

If your friend tells you their number is on cards A, B, C, and F, add: 1 + 2 + 4 + 32 = 39. If your friend tells you their number is only on card C, you know it must be 4. If your friend tells you their number is on all cards, then add: 1 + 2 + 4 + 8 + 16 + 32 = 63.

Check-in

  1. Without looking at the cards, say which cards the following numbers are on:
    1. 17
    2. 31
    3. 45
  2. Explain why there are exactly 32 numbers on each card.
  3. Explain why zero doesn’t appear on any card.
  4. Explain why this game won’t work with octal or decimal—or any other base beside two.

Beyond positive integers

As we move beyond positive integers, we’ll need some new ways to represent negative numbers. For this game, they are excluded.

© 2025 Clayton Cafiero.

No generative AI was used in producing this material. This was written the old-fashioned way.