Introduction to binary representation of numbers
You may know that deep down, everything that goes on in a digital computer—everything that’s stored, everything that’s calculated, everything that’s displayed, etc.—is in binary form, that is, as strings of zeros and ones.
But what does that mean?
- How can zeros and ones represent a picture or a sound?
- How can zeros and ones represent the symbols we type at the keyboard and that we see displayed on the screen?
- How can we represent numbers as merely ones and zeros, and how can we do calculations with them?
- How are the computer’s instructions represented as zeros and ones?
Perhaps, the most significant question: Why just zeros and ones? Why not use other values instead?
These are important questions with interesting answers in every case.
- Ease of implementation in hardware
- Deep connection to the foundations of logic
- Simple (only two possible values)
A game of twenty questions
As a child (or perhaps more recently) it’s likely you’ve played a game of “twenty questions” (if you haven’t, don’t worry, the rules are quite simple). The game goes like this: one player thinks of something—a physical object, a person, a book, whatever, but keeps it secret in their head—and then the other player may ask up to twenty questions in order to discover the secret. But there’s a twist: all the questions must be answerable (and answered) with a simple “YES” or “NO”.
For example, I’m thinking of a giraffe, and my friend can ask twenty questions.
Q 1: Is it bigger than a microwave oven?
A: YES
Q 2: Is it bigger than the Empire State Building?
A: NO
Q 3: Is it a human artifact?
A: NO
Q 4: Is it alive?
A: YES
Q 5: Is it a plant?
A: NO
Q 6: Is it a mammal?
A: YES
Q 7: Does it live in Vermont?
A: NO
Q 8: Does it live in Africa?
A: YES
Q 9: Does it eat other animals?
A: NO
Q 10: Does it eat insects? (Kind of a throwaway question since insects are animals, but that’s how the game goes sometimes.)
A: NO
Q 11: (feeling emboldened) Is it an elephant?
A: NO
Q 12: Does it have stripes?
A: NO
Q 13: Is it taller than a human?
A: YES
Q 14: Did the 20th century surrealist painter Salvador Dalí ever make a painting of this animal?
A: YES
Q 15: Is it a giraffe?
A: YES
And the questioner wins! They’ve discovered the secret in 15 questions.
Twenty questions with numbers
Now what if I told you we could play this game a little differently? We’ll keep the twenty questions framework, but instead of arbitrary objects, we’re going to play this game with numbers. OK. Are you ready? I’m thinking of a number between one and 1,048,576.
“Wait! What?” you think. “I can’t discover the secret number in just twenty guesses.”
“But you can!” I insist. “Give it a little thought. There’s more than one winning strategy!”
You scratch your chin and say “Hmmmm”. (If you don’t already know at least one winning strategy, now would be a good time to really scratch your chin and say “Hmmmm” and give it some thought before proceeding.)
One strategy is to start by guessing in the middle. But we can’t just ask questions about individual numbers (yet). Our goal is to eliminate half of the numbers between one and 1,048,576 with a single question. But the question must admit only “YES” or answers “NO”. (Again, if you’re not sure how you might do this, please take a moment and give it some thought.)
Alright. Let’s say I’m thinking of 101,482 (I just picked at random).
Here’s how your questions would proceed with one winning strategy.
Q 1: Is it greater than or equal to 524,288?
A: NO
Where’d we get 524,288? It’s 1,048,576 divided by two. Right in the middle of the range. Since I’ve answered “NO”, you no longer need to consider any numbers greater than 524,287! Now you have 19 questions to discover the secret number that you now know must be between one and 524,287. Once again, you choose the number in the middle of the range.
Q 2: Is it greater than or equal to 262,145?
A: NO
Again, you’ve ruled out half of the numbers in the range with a single question. Do it again.
Q 3: Is it greater than or equal to 131,073?
A: NO
Now you know the secret number is between one and 131,072 and you have 17 questions remaining.
Q 4: Is it greater than or equal to 65,537?
A: YES
This is interesting. Now you know the number is between 65,537 and 131,072, and once again, you’ve eliminated half of the range. For the next question, you calculate the midpoint between these two bounds, that’s
(131,072 + 65,537 + 1) / 2 = 98,305
(and we’ll apply this formula as we go, and ignore any fractional part of the answer when asking questions).
Q 5: Is it greater than or equal to 98,305?
A: YES
Wonderful! Now you know that the number is between 98,305 and 131,072. Things are looking more manageable now, and you still have 15 questions remaining. Do it again: find the midpoint between these two and ask the next question.
(131,072 + 98,305 + 1) / 2 = 114,689
Q 6: Is it greater than or equal to 114,689?
A: NO
Now you know the number is between 114,688 and 98,305. Do it again.
(114,688 + 98,305 + 1) / 2 = 106,497.
Q 7: Is it greater than or equal to 106,497?
A: NO
Now you know the number is between 106,496 and 98,305. Do it again.
(106,496 - 98,305 + 1) / 2 = 102,401.
Q 8: Is it greater or equal to than 102,401?
A: NO
You proceed in like fashion, asking is the number greater than or equal to 100,353 (YES), 101,377 (YES), 101,889 (NO), 101,633 (NO), 101,505 (NO), 101,441 (YES), 101,473 (YES), 101,489 (NO), 101,481 (YES).
At this point, after 17 questions we know that the secret number is between 101,481 and 101,488.
Q 18: Is it greater than or equal to 101,485?
A: NO
Q 19: Is it greater than or equal to 101,483?
A: NO
Q 20: (Now you know for certain!) Is it 101,482?
A: YES
Boom! You’ve discovered the secret number from among over a million possibilities in exactly 20 guesses. Cool, huh?
Why does this work? The original upper bound, 1,048,576, is a power of two.
2^{20} = 1,048,576
That’s multiplying by two twenty times.
\begin{align*} 1 \times 2 &= 2 &(2^1) \\ 2 \times 2 &= 4 &(2^2) \\ 2 \times 4 &= 8 &(2^3) \\ 2 \times 8 &= 16 &(2^4) \\ 2 \times 16 &= 32 &(2^5) \\ 2 \times 32 &= 64 &(2^6) \\ 2 \times 64 &= 128 &(2^7) \\ 2 \times 128 &= 256 &(2^8) \\ 2 \times 256 &= 512 &(2^9) \\ 2 \times 512 &= 1,024 &(2^{10}) \\ 2 \times 1,024 &= 2,048 &(2^{11}) \\ 2 \times 2,048 &= 4,096 &(2^{12}) \\ 2 \times 4,096 &= 8,192 &(2^{13}) \\ 2 \times 8,192 &= 16,384 &(2^{14}) \\ 2 \times 16,384 &= 32,768 &(2^{16}) \\ 2 \times 32,768 &= 65,536 &(2^{16}) \\ 2 \times 65,536 &= 131,072 &(2^{17}) \\ 2 \times 131,072 &= 262,144 &(2^{18}) \\ 2 \times 262,144 &= 524,288 &(2^{19}) \\ 2 \times 524,288 &= 1,048,576 &(2^{20}) \end{align*}
Now think about it? How many times can we divide by two before we’re back to where we’ve started? Twenty.
So if at every step in our game of twenty questions, the questioner effectively divides the search space in half, how many times can we do this before we winnow things down to a single number—the secret number? At most, twenty. That’s a winning strategy.
This is such a powerful technique that it has a name: binary search. At each step, we cut the search space in half.
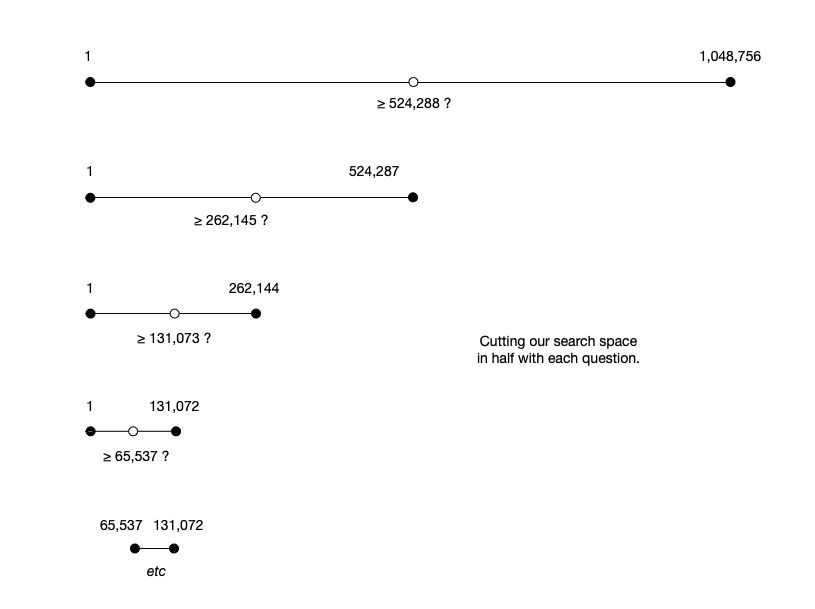
Hopefully, this will give you a sense of the power of powers of two—the foundation of binary numbers and binary arithmetic.
Check in
Let’s say I’m thinking of a secret number between one and 65,536.
- How many questions would you need to guarantee you’d be able to determine the secret number?
- What would your first question be?
Different number systems
We’ll take a little detour here to explain different representation of numbers, and introduce the octal and binary systems, and then return to our game of twenty questions with another winning strategy.
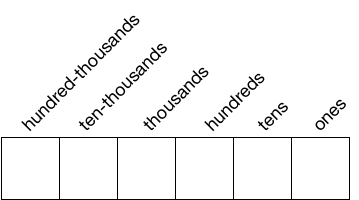
As you are no doubt aware, we use a base 10 or decimal system of representing numbers. Our system is positional. Digits appear in positions and their values depend on their position. That is, we have a ones column, a tens column, a hundreds column and so on.
But that’s not the only way to write or represent numbers. Back in ancient times and other parts of the world, many different ways were invented to represent numbers. Some were base 10, some weren’t. Some were mostly positional, many weren’t. These worked in a rudimentary way, but they didn’t make calculation very easy.
For example, the Babylonians had a base 60 counting system written in cuneiform. Unlike our familiar decimal system, they had 59 non-zero digits. Their system was positional, but not completely so. They did not have a way to write zero, and so the same symbol in their system might represent different values depending on context.
The ancient Egyptians had few different systems that were more-or-less base 10, but awkwardly written in hieroglyphs (and don’t get me started about Egyptian fractions—yikes!). Their system was not positional. Despite that, I particularly like their hieroglyph for one million or any very large number:
(It looks to me like the little fellow is throwing up his hands in frustration.) These symbols served their purposes but they were awkward indeed.
The Romans had their own system which was, well, special. They had an algorithm for multiplication, but it was terribly complicated. How would you multiply \text{XLII} by \text{CXIV} (42 \times 114) using only their system? Yeah, me neither.
One thing notably missing from the Babylonian, Egyptian, and Roman systems is a symbol for zero. Zero, as a symbol in a positional system, was invented by Indian mathematicians some time between 0 CE and 300 CE, and comes to us—and the vast majority of the world today—via Arabic and Persian mathematicians from around the 9th century. Thus, our system is known as the Hindu–Arabic numeral system.
In this system, we have a fixed number of digits: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, and each digit’s value depends on its position, with each position representing a power of ten.
The number 31,605 can be expanded
\begin{align*} 0 \times 10^5 &=& \phantom{00,000}0 \\ 3 \times 10^4 &=& 30,000 \\ 1 \times 10^3 &=& 1,000 \\ 6 \times 10^2 &=& \phantom{0}600 \\ 0 \times 10^1 &=& \phantom{00,000}0 \\ 5 \times 10^0 &=& \phantom{00,000}5 \\ \hline & & 31,605 \end{align*}
(Recall that by definition, anything to the zero power is one.) Going back to our earlier illustration, we can fill in the values for 31,605 (decimal).
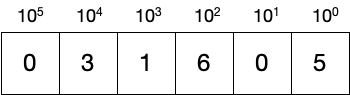
Notice what zero gets us: a fully positional system. Zero is used to show there is no value for the corresponding power of the base.
Other bases
Now, a typical human has ten fingers so it seems quite likely that a decimal, base 10, numeral system had its roots in counting on one’s fingers. But there’s nothing mathematically special about ten.
I don’t know if octopodes (the plural of “octopus”) can count, but if they can, and if they use a positional numeral system, then it’s likely they’d use eight as a base, and not ten.

Let’s suppose that octopodes can count, and that they do in fact use a positional numeral system when they write (yes, I know, indulge me). Instead of digits 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, they’d have digits for 0, 1, 2, 3, 4, 5, 6, 7, and instead of each position representing a power of ten, each position would represent a power of eight. So if you were an octopus mathematician you’d write things differently—you’d use an octal (base eight) system.
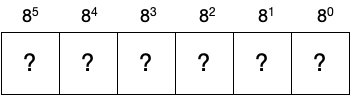
Counting up all the tentacles on your body and the body of your friend would go like this:
1, 2, 3, 4, 5, 6, 7, 10, 11, 12, 13, 14, 15, 16, 17, 20.
We’re so used to a decimal system that it looks like numbers are being left out and that, for example, “10” means 10, but that’s not so. In octal, “10” means one eight and zero ones (equivalent to decimal eight), and “20” means two eights and zero ones (equivalent to decimal 16).
Now let’s consider how we’d write 31,605 decimal in octal.
The octal equivalent for 31,605 (decimal) is 75,565 (octal). It’s absolutely crucial that you understand these aren’t two different numbers, they’re just two different ways of writing the exact same number.
31,605 \text{ (decimal)} = 75,565 \text{ (octal)}.
Let’s break it down.
\begin{align*} 0 \times 8^5 &=& \phantom{00,000}0 \\ 7 \times 8^4 &=& 70,000 \\ 5 \times 8^3 &=& 5,000 \\ 5 \times 8^2 &=& \phantom{0}500 \\ 6 \times 8^1 &=& \phantom{00,000}6 \\ 5 \times 8^0 &=& \phantom{00,000}5 \\ \hline & & 75,565 \end{align*}
Keep in mind that all the numbers immediately above are in octal not decimal.
Check in
- What is 42^0?
- How would you write 123 in octal?
- The Maya had a base 20 numeral system. How many digits would you need to write numbers in a positional, base 20 numeral system?
The binary system
We’ve seen that we can use different bases to represent numbers in different positional numeral systems. Now let’s look at the binary system. The binary system is base two, and thus has only two digits: 0 and 1. Each position in this system corresponds to a power of two.
How would we count in this system?
0, 1, 10, 11, 100, 101, 110, 111, 1000, 1001, 1010, 1011, 1100, 1101, 1111, \ldots
As decimal equivalents, we have:
| binary | decimal |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 10 | 2 |
| 11 | 3 |
| 100 | 4 |
| 101 | 5 |
| 110 | 6 |
| 111 | 7 |
| 1000 | 8 |
| 1001 | 9 |
| 1010 | 10 |
| 1011 | 11 |
| 1100 | 12 |
| 1101 | 13 |
| 1110 | 14 |
| 1111 | 15 |
Let’s break down a slightly greater number 101011.
\begin{align*} 1 \times 2^5 &=& 32 \\ 0 \times 2^4 &=& 0 \\ 1 \times 2^3 &=& 8 \\ 0 \times 2^2 &=& 0 \\ 1 \times 2^1 &=& 2 \\ 1 \times 2^0 &=& 1 \\ \hline & & 43 \end{align*}
We can take this approach to expand our table (above), hopefully by way of clarification.
| binary | decimal | |
|---|---|---|
| 0 | 0 \times 2^0 | 0 |
| 1 | 1 \times 2^0 | 1 |
| 10 | 1 \times 2^1 + 0 \times 2^0 = 2 + 0 | 2 |
| 11 | 1 \times 2^1 + 1 \times 2^0 = 2 + 1 | 3 |
| 100 | 1 \times 2^2 + 0 \times 2^1 + 0 \times 2^0 = 4 + 0 + 0 | 4 |
| 101 | 1 \times 2^2 + 0 \times 2^1 + 1 \times 2^0 = 4 + 0 + 1 | 5 |
| 110 | 1 \times 2^2 + 1 \times 2^1 + 0 \times 2^0 = 4 + 2 + 0 | 6 |
| 111 | 1 \times 2^2 + 1 \times 2^1 + 0 \times 2^0 = 4 + 2 + 1 | 7 |
| 1000 | 1 \times 2^3 + 0 \times 2^2 + 0 \times 2^1 + 0 \times 2^0 = 8 + 0 + 0 + 0 | 8 |
| 1001 | 1 \times 2^3 + 0 \times 2^2 + 0 \times 2^1 + 1 \times 2^0 = 8 + 0 + 0 + 1 | 9 |
| 1010 | 1 \times 2^3 + 0 \times 2^2 + 1 \times 2^1 + 0 \times 2^0 = 8 + 0 + 2 + 0 | 10 |
| 1011 | 1 \times 2^3 + 0 \times 2^2 + 1 \times 2^1 + 1 \times 2^0 = 8 + 0 + 2 + 1 | 11 |
| 1100 | 1 \times 2^3 + 1 \times 2^2 + 0 \times 2^1 + 0 \times 2^0 = 8 + 4 + 0 + 0 | 12 |
| 1101 | 1 \times 2^3 + 1 \times 2^2 + 0 \times 2^1 + 1 \times 2^0 = 8 + 4 + 0 + 1 | 13 |
| 1110 | 1 \times 2^3 + 1 \times 2^2 + 1 \times 2^1 + 0 \times 2^0 = 8 + 4 + 2 + 0 | 14 |
| 1111 | 1 \times 2^3 + 1 \times 2^2 + 1 \times 2^1 + 1 \times 2^0 = 8 + 4 + 2 + 1 | 15 |
Check in
- In the table above, we see that the greatest number we can represent with one (binary) digit is one, the greatest number we can represent with two digits is three, the greatest number we can represent with three digits is seven, and so on. What’s the greatest number we can represent with six digits?
- Let b = 2 be the base of some numeral system, and let n be some number of digits. Can you write a formula that would give you the greatest number that can be represented with n digits for any arbitrary positive integer n?
- How can we immediately tell if a binary number is even or odd?
- How can we immediately tell if a binary number is a power of two?
- In a decimal system, how can we immediately tell if a number is a power of ten?
- In a decimal system, how can we immediately tell if a number is a multiple of ten?
Let’s go over the answers to the check in questions above.
- In a binary system the greatest number we can represent with six digits is 1 \times 2^5 + 1 \times 2^4 + 1 \times 2^3 + 1 \times 2^2 + 1 \times 2^1 + 1 \times 2^0 = 32 + 16 + 8 + 4 + 2 + 1 = 63.
- b^n - 1. Notice that our answer for #1 (above) was 63—the greatest number we can represent with six binary digits. That’s exactly 2^6 - 1. This formula holds for any integer b \geq 2 and any positive integer n. Try it out with octal numbers. What’s the greatest number we can represent with seven octal digits? 8^7 - 1 = 2,097,151. Try a different base. What’s the greatest number we can represent in with nine digits in a base five system? 5^9 - 1 = 1,953,124. Feel free to verify these results with a pocket calculator.
- The least significant digit in a binary number is either zero or one. If this digit is zero, the number is even; if this digit is one, the number is odd. Easy, huh?
- We can immediately tell if a binary number is a power of two if it has a single digit one (in any position) and all other digits are zero. So, for example, 1, 10, 100, 1000, 10000, are all powers of two.
- It works the same way for decimal digits. If a decimal number has a single one followed by any number of zeros, it’s a power of ten: 1, 10, 100, 1000, 10000. See a pattern here?
- In a decimal system, a number is a multiple of ten if it has a zero in the ones place.
Addition and multiplication tables
You may have been expected to memorize addition and multiplication tables as a kid. Here they are for our decimal counting system.
Addition
| + | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 2 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 3 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 4 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 5 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 6 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 7 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 8 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 9 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
Multiplication
| \times | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 2 | 0 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 |
| 3 | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 |
| 4 | 0 | 4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 |
| 5 | 0 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 |
| 6 | 0 | 6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 | 54 |
| 7 | 0 | 7 | 14 | 21 | 28 | 35 | 42 | 49 | 56 | 63 |
| 8 | 0 | 8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 | 72 |
| 9 | 0 | 9 | 18 | 27 | 36 | 45 | 54 | 63 | 72 | 81 |
We won’t get into binary arithmetic just yet (but soon enough). Nevertheless, let’s take a look at addition and multiplication tables for the binary counting system.
Addition
| + | 0 | 1 |
|---|---|---|
| 0 | 0 | 1 |
| 1 | 1 | 10 |
Multiplication
| \times | 0 | 1 |
|---|---|---|
| 0 | 0 | 1 |
| 1 | 1 | 1 |
Wow. That’s all there is to these tables. File this away for now, but soon we’ll see how powerful this becomes inside your computer.
Another winning strategy
Now that we’ve had our whirlwind tour of numeral systems—decimal, octal, and binary—we’re ready to revisit our game of twenty questions for numbers. An understanding of binary numbers will open up an entirely new approach.
As you recall, in the earlier example, we asked questions in a way that allowed us to cut our search space in half at each step. However, there’s a different way we can go about it, and still have a winning strategy. Instead of asking questions of the form “Is the number greater than or equal to x?” for some x, we can ask a little differently.
Again, I’m thinking of a number between one and 1,048,576, and let’s say this secret number is the same one we used earlier, 101,482, and again the other player has twenty questions available.
Knowing what you know now about binary representation, can you think of twenty questions that would uniquely determine a number in this interval?
Sure, we just ask about the binary representation!
To really drive the point home, we’ll number the questions from 0 to 19 instead of 1 to 20 (the reason should become clear as we proceed), and we’ll indicate how we construct the binary representation as we go. We’ll also leave a blank space every four digits to ease reading.
Q 0: Does the binary representation of the secret number have a 1 in the 2^0 place?
A: NO. (So far, we can construct 0.)
Q 1: Does the binary representation of the secret number have a 1 in the 2^1 place?
A: YES (So far, we can construct 10.)
Q 2: Does the binary representation of the secret number have a 1 in the 2^2 place?
A: NO (So far, we can construct 010.)
Q 3: Does the binary representation of the secret number have a 1 in the 2^3 place?
A: YES (So far, we can construct 1010.)
Q 4: Does the binary representation of the secret number have a 1 in the 2^4 place?
A: NO (So far, we can construct 0 1010.)
Q 5: Does the binary representation of the secret number have a 1 in the 2^5 place?
A: YES (So far, we can construct 10 1010.)
Q 6: Does the binary representation of the secret number have a 1 in the 2^6 place?
A: YES (So far, we can construct 110 1010.)
Q 7: Does the binary representation of the secret number have a 1 in the 2^7 place?
A: NO (So far, we can construct 0110 1010.)
Q 8: Does the binary representation of the secret number have a 1 in the 2^8 place?
A: NO (So far, we can construct 0 0110 1010.)
Q 9: Does the binary representation of the secret number have a 1 in the 2^9 place?
A: NO (So far, we can construct 00 0110 1010.)
Q 10: Does the binary representation of the secret number have a 1 in the 2^{10} place?
A: YES (So far, we can construct 100 0110 1010.)
Q 11: Does the binary representation of the secret number have a 1 in the 2^{11} place?
A: YES (So far, we can construct 1100 0110 1010.)
Q 12: Does the binary representation of the secret number have a 1 in the 2^{12} place?
A: NO (So far, we can construct 0 1100 0110 1010.)
Q 13: Does the binary representation of the secret number have a 1 in the 2^{13} place?
A: NO (So far, we can construct 00 1100 0110 1010.)
Q 14: Does the binary representation of the secret number have a 1 in the 2^{14} place?
A: NO (So far, we can construct 000 1100 0110 1010.)
Q 15: Does the binary representation of the secret number have a 1 in the 2^{15} place?
A: YES (So far, we can construct 1000 1100 0110 1010.)
Q 16: Does the binary representation of the secret number have a 1 in the 2^{16} place?
A: YES (So far, we can construct 1 1000 1100 0110 1010.)
Q 17: Does the binary representation of the secret number have a 1 in the 2^{17} place?
A: NO (So far, we can construct 01 1000 1100 0110 1010.)
Q 18: Does the binary representation of the secret number have a 1 in the 2^{18} place?
A: NO (So far, we can construct 001 1000 1100 0110 1010.)
Q 19: Does the binary representation of the secret number have a 1 in the 2^{19} place?
A: NO (That’s the twentieth and last digit, so we now have 0001 1000 1100 0110 1010.)
That’s our answer: 0001 1000 1100 0110 1010 (binary)! Notice that there are only two possible answers for each digit. If the answer is “YES” we have a 1 in that place; if the answer is “NO” we have a 0.
Let’s convert this to decimal to verify the result.
\begin{align*} &0 \times 2^{19} &= \phantom{000,00}0 &\hspace{1em}\text{(decimal)} \\ + &0 \times 2^{18} &= \phantom{000,00}0 & \\ + &0 \times 2^{17} &= \phantom{000,00}0 & \\ + &1 \times 2^{16} &= \phantom{0}65,536 & \\ + &1 \times 2^{15} &= \phantom{0}32,768 & \\ + &0 \times 2^{14} &= \phantom{000,00}0 & \\ + &0 \times 2^{13} &= \phantom{000,00}0 & \\ + &0 \times 2^{12} &= \phantom{000,00}0 & \\ + &1 \times 2^{11} &= \phantom{00}2,048 & \\ + &1 \times 2^{10} &= \phantom{00}1,024 & \\ + &0 \times 2^{9} &= \phantom{000,00}0 & \\ + &0 \times 2^{8} &= \phantom{000,00}0 & \\ + &0 \times 2^{7} &= \phantom{000,00}0 & \\ + &1 \times 2^{6} &= \phantom{000,0}64 & \\ + &1 \times 2^{5} &= \phantom{000,0}32 & \\ + &0 \times 2^{4} &= \phantom{000,00}0 & \\ + &1 \times 2^{3} &= \phantom{000,00}8 & \\ + &0 \times 2^{2} &= \phantom{000,00}0 & \\ + &1 \times 2^{1} &= \phantom{000,00}2 & \\ + &0 \times 2^{0} &= \phantom{000,00}0 & \\ \hline & & 101,482 & \end{align*}
Look at that. With a binary system, we can construct a number from a series of YES / NO questions. That’s very interesting.
Check in
- Explain why we can’t fully determine an n digit number with a sequence of n YES / NO questions for any base greater than two.
Summary
Here we’ve seen that there’s more than one way to represent a number and in one sense the choice of base is arbitrary. However, in the case of a binary numeral system, each power of two is represented by a 0 or 1. Those are the only digits available!
We’ve also seen that the addition and multiplication tables are quite simple. There’s not much to binary arithmetic (we’ll learn more about this soon).
Of course, there’s much detail that we’ve left out here, for example:
- How do we represent positive and negative integers in a binary system?
- How do we represent fractions or numbers with something to the right of the decimal point in a binary system?
- How large or small can numbers be on a given computer?
- Are there other things that can be represented as strings of zeros and ones?
- What other advantages are there of binary systems?
© 2025 Clayton Cafiero.
No generative AI was used in writing this material. This was written the old-fashioned way.