|
Introduction
Berkeley
Madonna
is designed to numerically solve systems of ordinary differential
equations as fast as possible. By compiling textual equations into
machine code, it achieves execution speeds approaching that of
handwritten C or FORTRAN code. Models are quickly constructed with
Berkeley Madonna's easy-to-use equation editor. Or you can use the new
flowchart editor to build models graphically.
Berkeley Madonna was originally
developed to run STELLA® models faster. As a result, it is capable of
running many existing STELLA models with little or no modification.
Simply save your STELLA model's equations as text and open them in
Berkeley Madonna.
Features
Solves:
- Ordinary Differential Equations - initial conditions and boundary
value problems
- Difference Equations - initial conditions and boundary value
problems
- Multi-dimensional transcendental algebraic equation roots
- Discrete simulations using conveyors, ovens, and queues
Easy to Use:
- Type equations directly into equation window in ordinary
mathematical notation, in any order;
or, import equations from STELLA equation files.
- Click Run. Solutions are automatically plotted. Buttons on
toolbar allow variables to be toggled on and off the graph.
Special Interfaces:
- Flowchart
Editor - create models visually with icons and let Berkeley
Madonna write the equations.
- Chemical
Reactions - write chemical equations using conventional chemical
notation. Berkeley Madonna will automatically apply the appropriate
rate law (e.g., mass action) and generate kinetic equations for you.
Very Fast Execution:
- Berkeley Madonna's impressive speed makes it suitable for
large-scale systems, boundary value problems, Monte Carlo models,
curve fitting, root finding, batch processes, parameter plots, stiff
systems, etc.
Parameter Exploration:
- Change parameter values directly using the parameter window.
- Parameter Sliders - move the slider and the model runs instantly
and displays the new solution.
- Automatic Scan of Parameter Space - define a range for a parameter
and Berkeley Madonna computes and plots a family of curves spanning
the range.
- Parameter Plots - select an attribute (min, max, mean, frequency,
etc.) of any variable. Berkeley Madonna automatically plots the
attribute as a function of a parameter.
- Sensitivity Analysis - plots the partial derivative of any
variable with respect to any parameter.
- Optimization - searches the parameter space for a point that
minimizes an arbitrary expression.
Integration Algorithms:
- Euler (1st-order)
- Runge-Kutta (2nd and 4th order)
- Adaptive stepsize (4th order Runge-Kutta)
- Stiff ODE solver (Rosenbrock)
- Custom DT - write your own equations for adjusting stepsize
Import Experimental Data:
- Use imported data sets as piecewise-linear functions in your
model.
- Curve Fitter - estimate parameters by fitting solution to one or
more data sets
Other Capabilities:
- Fast Fourier Transform - plot results in frequency domain.
- Array notation (dimensioned variables)
- Hybrid multi-dimensional root solver used to automatically set up
steady-state initial conditions. Can also be embedded in integration
loops.
Intuitive Interface:
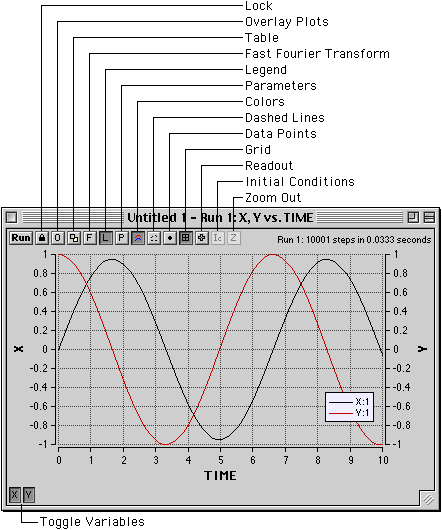
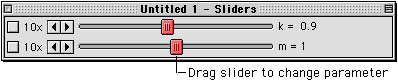
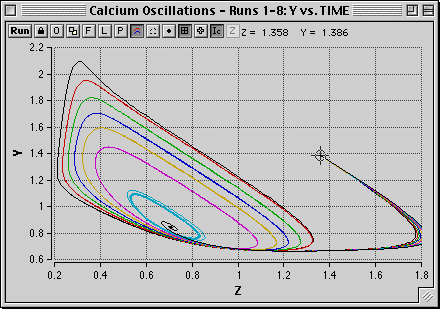
Phase Plane (X-Y) Plots:
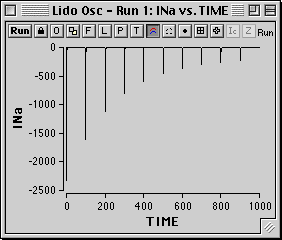
Oscilloscope Plots:
 |
 |
| Normal plot |
Oscilloscope plot
User-defined triggers reset plot to time zero. |
|




