Mapped forest mortality is an assessment of the total area of current-year tree mortality across the landscape.
Forest Mortality scored out of 5 in 2018
For this indicator, the score is given for the latest year of the dataset, which was 2018 for Forest Mortality. The score is calculated using a target value and the historical range of the the entire long-term dataset. The higher the score, the closer this year's value is to the target.
Forest Mortality scores are
Once the score is computed for each year, the trend in scores over time is calculated. If the trend is significantly positive or negative, the long-term trend is marked as increasing or decreasing respectively.
Details on how the targets and scores are calculated for this indicator are shown below:
| Calculation Component | Description |
|---|---|
| Latest Year of Data Available | 2018 |
| Scored as | Distance between minimum and maximum (scored 0-1) |
| Target value | Data minimum |
| Directionality of scores | Lower values in the data are better |
| Minimum value used in scoring | Data minimum - 10% of the range |
| Maximum value used in scoring | Data maximum + 10% of the range |
| View in FEMC Archive | Dataset: Vermont ADS Standardized Data for Indicators Dashboard |
Forest ecosystems are complex. They provide us jobs and timber products, all the while storing carbon, improving water quality, and creating wildlife habitat, among many other important provisions. Using datasets related to forest health, we have created four easy to interpret indices to provide an understanding of the health of our forests in four areas: Structure, Condition, Services, and Stressors. Using high-quality datasets, we computed annual scores for each metric of forest health, including a score depicting where it falls in relation to the desired value. A score closer to 5 suggests a higher functioning or healthier forest condition. We also provide an assessment of the long-term trends, where a red circle indicates a worsening, yellow no change, and green an improved condition over time.
The purpose of the Forest Indicators Dashboard is to:
The Forest Indicators Dashboard (FID) grew from a working group coordinated by Dr. Jennifer Pontius (University of Vermont, Forest Ecosystem Monitoring Cooperative) at the 2015 Annual Conference of the Vermont Monitoring Cooperative (now Forest Ecosystem Monitoring Cooperative, FEMC). The aim was to develop a tool to be used by decision-makers, educators, and the general public to capture the condition of Vermont’s forest ecosystem as well as provide a long-term context for those changes. Following this initial working group meeting, FEMC staff worked with collaborators within the FEMC network to identify datasets and establish criteria for scoring to be used in the dashboard.
The Forest Indicators Dashboard has four indicator categories: Structure, Condition, Services, and Stressors. Within each of these categories, there are multiple datasets that have been selected to best represent the category. The datasets selected characterize the forested ecosystem in objectively measurable ways and come from high quality, long-term sources. They are easily measured and available on an regular basis (preferably annual), and further, must come from sources with stable funding to ensure ongoing collection. The datasets that drive this dashboard are dynamic, meaning that they are updated with new monitoring on a regular basis. The datasets within each of the for indicator categories are averaged based on a stakeholder-defined weighting, producing an Overall Score with a scale of 1 (impaired status) to 5 (optimum status).
Metrics included in the Forest Indicators Dashboard were selected through an expert working group, as well as based on data availability and quality. We sought to include a limited number of datasets per category, while providing a robust assessment of forest health based on a suite of measurements.
Periodic values for each metric produce a current condition value for the most recent year of the data, such as the current forest growth rate or total annual precipitation. These values are translated into scores on a 1 to 5 scale to provide an estimate of whether things are getting ‘better’ or ‘worse’. To generate the current year’s score, this value is compared to a target value. For example, for Hardwood Regeneration, the current-year value is scored based on where it falls between the minimum and maximum hardwood regeneration values in the entire dataset, and the target is higher regeneration. Higher hardwood regeneration density in any year thus receives a higher score. Conversely, for maximum annual temperature, the current-year score is computed as the distance away from the long-term mean, as deviations away from historical patterns can negatively affect forests. The closer the value for a given year is to the long-term mean, the higher the score will be. More specific details on the target, maximum, and minimum values, as well as computational notes are included with each metric. For more information, refer to our comprehensive methodology.
For many metrics, the computation of annual scores is dynamic. This means that as new data becomes available and is added to the FID, previously calculated annual scores may change. If the annual scores are computed relative to the long-term mean, this addition of a new year of data could change the long-term mean and thus, the resultant annual scores. Because the scores could change from year to year, we offer snapshots of the dashboard over time, allowing you to revisit previous versions of the dashboard.
Computation of annual scores is often limited by data availability. For some datasets, we may alter annual score computation to be more ecologically relevant. For example, we may change the annual score computation from a deviation from the long-term mean to a deviation from a baseline.
We did not assess non-linear trends. The significance of each long-term trend was tested using linear regression and a p-value threshold of 0.05.
Below are detailed descriptions of our methodology used to process and analyze the datasets included in FID. For each, we describe the data source, the data processing, the target value, and computation of the annual score.
In the example below, we present graphs of data (blue solid line) and the trend of these data (blue dotted line) for three different time periods (2004-2015, 2004-2016, and 2004-2017). For these data, the target was set to be the long-term mean (red line). Notice that as new data are added each year (moving from 2015-2017 in the figures below), the target dynamically changes. The upper and lower scoring bounds (grey lines) were set to be the minimum value in the dataset -10% of the range and the maximum value in the dataset +10% of the range, respectively. Like for the target, as new data are included each year, these bounding values also change. In the example below, values for 2016 and 2017 are higher than in the rest of the dataset, so that the upper scoring bound increases as these years of data are added.
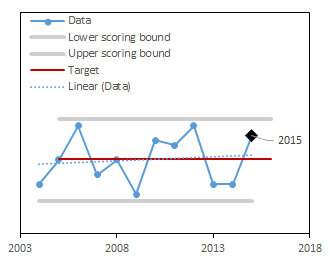
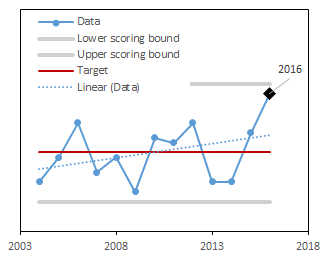
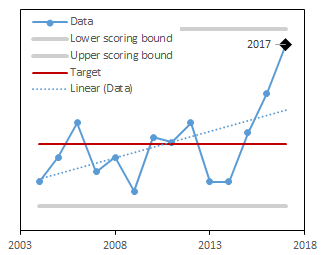
We used forest cover estimates generated by Forest Inventory and Analysis program accessed via the FIA Datamart Access Database1. We relied on the query and methods set by FIA to compute these estimates. We then converted them to a percentage of the state of Vermont using the total area of the state. The target was set as the long-term mean value. The annual score was computed as a deviation from the target, scaled to be between 0-1. When values were above the target, a score of 1 corresponds to the target and a score of 0 corresponds to the upper scoring bounds (maximum plus 10% of the range). When values were below the target, a score of 1 corresponds to the target and a score of 0 corresponds to the data lower scoring bounds (minimum minus 10% of the range).
We collected counts of sugar maple (Acer saccharum) seedlings per subplot in the Forest Inventory and Analysis Phase 2 plots via the FIA Datamart Access Database1. The first year of available data is 2003. A hardwood seedling is classified as a small tree less than 1" in diameter and greater than 12" in height2. We averaged seedling counts over all sampled subplots per year and scaled this number to the acreage of a subplot (0.25 ac.) to compute a density value (seedlings per acre). Per FIA protocol, plots are reassessed every 5 years until 2014, and every 7 years after that. To compute the annual score, we used 5-year leading edge moving window (i.e., data reported for 2007 used 2003, 2004, 2005, 2006 and 2007) until 2014 when we switched to a 7-year leading edge moving window per FIA protcol2. The target for this dataset was set to the maximum value plus 10% of the range. The score was then computed as the difference between the lower scoring bound of 0 and the target, scaled to be between 0-1.
We collected counts of red spruce (Picea rubens) seedlings per subplot in the Forest Inventory and Analysis Phase 2 plots via the FIA Datamart Access Database1. The first year of available data is 2003. A softwood seedling is classified as a small tree less than 1" in diameter and greater than 6" in height2. We averaged seedling counts over all sampled subplots per year and scaled this number to the acreage of a subplot (0.25 ac.) to compute a density value (seedlings per acre). Per FIA protocol, plots are reassessed every 5 years until 2014, and every 7 years after that. To compute the annual score, we used 5-year leading edge moving window (i.e., data reported for 2007 used 2003, 2004, 2005, 2006 and 2007) until 2014 when we switched to a 7-year leading edge moving window per FIA protcol2. The target for this dataset was set to the maximum value plus 10% of the range. The score was then computed as the difference between 0 and the target, scaled to be between 0-1.
Using Forest Inventory and Analysis data on Phase 1 plots accessed via the FIA Datamart Access Database1, we computed tree size class diversity using a Shannon-Weiner Diversity Index calculation (see equation below). The first available data year was 1997. We divided all sampled trees into 5 inch classes and tallied the total proportion of each size class measured in the plots. To compute the annual score, we used 5-year moving windows centered on the target year (i.e., data reported for 2005 used 2003, 2004, 2005, 2006 and 2007). This 5-year moving window was selected because FIA data is collected on a 5-year rotation. However, when the target year occured at the beginning or end of the time period, we used a smaller window. For instance, target year 2003 uses 2003, 2004, 2005, and target year 2004 uses 2003, 2004, 2005, 2006. This pattern is similar on the upper end of the data time period. The one exception is the 1997 data, which represented a full inventory, so no moving window was used to calculate values for this year. The target for this dataset was set as the maximum value plus 10% of the range. The annual score was then calculated as a deviation between the target and the lower scoring bounds (minimum value in the dataset minus 10% of the range), scaled to be between 0-1.
Shannon-Weiner Index (H’)
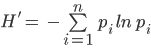
Where pi is the proportion of trees in the ith size class
From the Forest Cover images we generated (see details under that metric above), we used FragStats1 to compute the mean size of forest patches. While the first available year of data was 1992, we excluded this year from our analysis as NLCD methodology changed between 1992 and 2006. We used the the 8 cell neighborhood rule with a ‘no sampling’ strategy. We selected all Area-Edge Class metrics for computation.. We set the target for this dataset to be the long-term mean. The annual score was computed as the difference between the minimum (minimum value minus 10% of the range) and the target when values are below the target, or the upper scoring bounds (maximum value plus 10% of the range) and the target when values are above the target, scaled to be between 0-1.
From the Forest Cover images we generated (see details under that metric above), we used FragStats1 to compute the mean forest connectivity between forest blocks. While tThe first available year of data was 1992, we excluded this year from our analysis as NLCD methodology changed between 1992 and 2006. We used the the 8 cell neighborhood rule with a ‘no sampling’ strategy. We selected ‘Contagion’ as the Landscape Aggregation metric to compute. We set the target for this dataset to be the long-term mean. The annual score was computed as the difference between the lower scoring bounds (minimum value minus 10% of the range) and the target when values are below the target, or the upper scoring bounds (maximum value plus 10% of the range) and the target when values are above the target, scaled to be between 0-1.
Using Forest Inventory and Analysis data on Phase 1 plots via the FIA Datamart Access Database1, we tallied the number of trees (>5 in diameter) per species to compute a Shannon-Weiner Diversity Index (H’) (see equation below). The first year of available data was 1997. To compute the annual score, we used 5-year moving windows centered on the target year (i.e., data reported for 2005 used 2003, 2004, 2005, 2006 and 2007). This 5-year moving window was selected because FIA data is collected on a 5-year rotation. However, when the target year occured at the beginning or end of the time period, we used a smaller window. For instance, target year 2003 uses 2003, 2004, 2005, and target year 2004 uses 2003, 2004, 2005, 2006. This pattern is similar on the upper end of the data time period. The one exception is the 1997 data, which represented a full inventory, so no moving window was used to calculate values for this year. We set the target for this dataset at 3.5 according to established research2. The current year is scored as the distance between the acceptable species diversity thresholds of 1.5 and 3.52, scaled to be between 0 and 1.
Shannon-Weiner Index (H’)
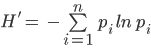
Where pi is the proportion of trees in the ith size class
Data on the annual acreage occupied by forests divided into 20 year age classes were extracted from the the Forest Inventory and Analysis EVALIDator1. The first year of available data was 2011. We re-catogorized stand ages into 40 year buckets (0-40, 40-80, and 80+ years) and created a ratio per each age class per year based on the estimated forestland. Per FIA protocol, plots are reassessed every 5 years until 2014, and every 7 years after that. The target for this dataset was set to the long-term mean, and the score was then computed as the deviation from this target, scaled to be between 0-1.
Crown dieback is a visual assessment of the percentage of the tree’s crown that has recent fine twig mortality. Crown dieback has been assessed annually on Vermont Forest Health Monitoring1 (FHM, a collaboration between FEMC and VT FPR) and North American Maple Project (NAMP) plots2 For the FHM program, plots have been assessed annually since 1994, but between 2008 and 2013, plots were assessed on a 3-year rotation. To generate values for the missing years of 2009 and 2012, we used the average dieback from 2008-2010 and 2011-2013, respectively. FHM dieback scores were averaged per plot per year of survey data. NAMP plots have assessed on an annual basis, beginning in 1988. While maple species are the focus of the NAMP project, co-occurring species have also been assessed. To approach the unequal species composition on NAMP plots, we selected only those plots that had more than one tree of a non-maple species. We averaged dieback within species in a plot prior to averaging across plots. We then computed the mean crown dieback for all species across all plots. From this, we computed the mean crown dieback for all species across all sampled plots in both the FHM and NAMP datasets. For crown dieback, the target was set as the long-term mean. We computed the current year score was the distance between the target and the upper scoring bounds (maximum value in the dataset plus 10% of the range), scaled to be between 0-1. Values below the target were scored as 1.
Insect and Disease Surveys (IDS) are annual aerial surveys of forests conducted by the State of Vermont and the USDA Forest Service to map forest disturbance, including damage caused by insects, diseases, fire, and weather events1. While the program has been conducted for many decades in Vermont, the first year of digitally available data was 1995. This metric is computed as a sum of forest area identified with visible damage in a given year (excluding any areas identified as current-year mortality) that has occurred since the previous survey. We set the target for this dataset to be the minimum value in the dataset minus 10% of the range. The current year is scored as the difference between the target and the upper scoring bounds (maximum value in the dataset plus 10% of the range), scaled to be between 0-1.
Insect and Disease Surveys (IDS) are annual aerial surveys of forests conducted by the State of Vermont and the USDA Forest Service to map areas of tree mortality1. While the program has been conducted for many decades in Vermont, the first year of digitally available data is 1995. This metric is computed as a sum of total area mapped with visible mortality in a given year that has occurred since the previous survey. We set the target for this dataset to be the minimum value in the dataset minus 10% of the range. The current year is scored as the difference between the target and the upper scoring bounds (maximum value in the dataset plus 10% of the range), scaled to be between 0-1.
Data on the proportion of trees in Vermont’s forest considered non-growing stock were extracted from the USFS Forest Inventory and Analysis Program Access database1. We used a FIA-established queries (“T005_Number of growing-stock trees on forestland” and “T004_Number of all live trees on forestland”) to compute the ratio. We took the inverse of this ratio to obtain the percentage of live trees not classified as growing stock. FIA defines a “growing stock tree” as a live tree >5.0 inches (12.7 cm) DBH that meet (now or prospectively) regional merchantability requirements in terms of saw-log length, grade, and cull deductions, and excludes rough and rotten cull trees2. Annual data began in 1997. We relied on FIAs statistical models for computing this value over time. We set the target for this dataset as the long-term mean. The score was then computed as the deviation from the target, scaled to be between 0-1. When values were above the target, a score of 1 corresponds to the target and a score of 0 corresponds to the upper scoring bounds (data maximum plus 10% of the range). When values were below the target, a score of 1 corresponds to the target and a score of 0 corresponds to the lower scoring bounds(data minimum plus 10% of the range).
Data on tree growth were extracted from the USFS Forest Inventory and Analysis Program Access database1. We used FIA-established queries (“T032_Mortality of all live trees on forestland-treesPerYr” and “T004_Number of all live trees on forestland”) to compute the mortality rate percentage for trees >5 inch DBH on sampled plots. Annual data began in 2006. We relied on FIAs statistical models for computing this value over time. We set the target for this dataset as the long-term mean. The score was then computed as the deviation from the target, scaled to be between 0-1. When values were above the target, a score of 1 corresponds to the target and a score of 0 corresponds to the upper scoring bounds (data maximum plus 10% of the range). When values were below the target, a score of 1 corresponds to the target and a score of 0 corresponds to the lower scoring bounds(data minimum plus 10% of the range).
Data on tree growth were extracted from the USFS Forest Inventory and Analysis Program Access database1. We used a FIA-established query (“T025_Net growth of all live on forestland-cuftPerYr”) for net growth of live trees >5 inch DBH on sampled P1 plots. Annual data began in 2006. We relied on FIAs statistical models for computing this value over time. We set the target for this dataset as the long-term mean. The score was then computed as the deviation from the target, scaled to be between 0-1. When values were above the target, a score of 1 corresponds to the target and a score of 0 corresponds to the upper scoring bounds (data maximum plus 10% of the range). When values were below the target, a score of 1 corresponds to the target and a score of 0 corresponds to the lower scoring bounds(data minimum plus 10% of the range).
Using MODIS phenology remote sensing products, we selected the Time Integrated (TIN) Normalized Difference Vegetation Index (NDVI) to quantify maximum canopy greenness over a growing season1. Available TIN images began in 2001. We first excluded all pixels with a value of either 0 or 255. Using National Land Cover Dataset (2011), we created a forest cover layer by masking out all non-forest pixels (i.e., those not identified as forest/woody wetlands [values 41, 42, 43, 90]). We used this forest mask to compute the mean TIN and standard deviation of the mean TIN across all forest-cover pixels per year. We also computed the long-term mean over record. We set the target for this dataset as the maximum value plus 10% of the range. The current year score was computed as the difference between the lower scoring bounds (minimum value in the dataset minus 10% of the range) and the target, scored to be between 0-1.
Using data collected in the Vermont Forest Resource Harvest Report1, we presented the total quantity of timber harvested in Vermont per year, which is reported as cords of wood. We set the target for these data as the maximum value in the dataset plus 10% of the range. The annual score was computed as the difference between the lower scoring bounds (either the minimum value in the data minus 10% of the range or 0, whichever was greater) and the target. This difference was scaled 0-1.
Species richness was collected from Vermont Integrated Watershed Information System1. We selected one location, Ranch Brook (site #502032) in Underhill VT, where species richness metrics were computed for macroinvertebrates. Data from other locations in the state did not have annually-resolved data with a sufficient long-term record to warrant inclusion. We used the EPT Richness score as computed by the dataset authors2. EPT Richness is a count of the unique number of taxa identified in the sample that belong to a trio of particularly sensitive macroinvertebrate orders - Ephemeroptera (mayflies), Plecoptera (stoneflies), and Tricoptera (caddisflies). In cases where a specimen could not be identified to the species level, it was only counted as unique taxon if no other specimens were identified to that level or below. In some cases, there were multiple samples in a single year. In these cases, we took the mean of the EPT Richness scores as the value for the year. The target for these data was set to be the maximum value plus 10% of the range. The annual score was computed as the difference between the lower scoring bound of 0 (indicating no EPT taxa were identified) and the target. This difference was then scaled from 0-1.
We used data on the annual number of meals procured from harvesting big game animals (white-tailed deer, black bear, moose, and wild turkey), as reported by the Vermont Department of Fish and Wildlife1. We set the data target as the data maximum plus 10% of the range. The annual score was computed as the difference between the lower scoring bound of 0 (indicating that no hunting harvests were reported) and the target, scaled to be between 0-1.
Using a query set by the Forest Inventory and Analysis program (‘IPCC carbon total: all 5 pools on forestland’) access via the FIA Data Mart1. This query computed the total carbon storage (in MgT) on FIA plots across all carbon pools. The first available year of data was 1997. The data target was set at the maximum value in the dataset plus 10% of the range. The annual score was computed as the difference between the lower scoring bounds (minimum value in the data minus 10% of the range) and the target. This difference was then scaled between 0-1.
We used the total annual maple syrup revenue (in dollars) reported by the USDA National Agriculture Statistics Service1. We set the dataset target as the maximum value in the dataset plus 10% of range. The annual score was then computed as the distance between the the lower scoring bounds (either the minimum value in the data minus 10% of range or 0, whichever was greater) and the target. This difference was then scaled 0-1.
Data on camping and day use visitation counts per state park in Vermont were accessed from Vermont Department of Forest Parks and Recreation1. Note that these data do not contain all Vermont public lands visitation counts; for example, Camel’s Hump State Park is managed by the Green Mountain Club and those data are not collected by the state of Vermont. To process these data, we first classified each park parcel2 in the FPR dataset by the percent of forest cover using the National Land Cover Dataset3. Data spanned from 1936-2016. A total of 144 parks were include in 2016, but further back in time, fewer parks are represented. Thus, we select the years 1970-2016 to have >129 parks per year. The goal of this step was to subset state parks where forests were a predominant reason visitors came to the park, as opposed to water bodies or other types of non-forested natural resources. We classified parks based on the percent of Deciduous, Evergreen, and Mixed Forest Cover according to the NLCD (codes 41, 42, 43). We did not include Woody Wetland cover (code 90) because many parks that are adjacent to water bodies were classified as high amount of forest cover when this land cover type was included. Based on our familiarity with many of the State Parks, we selected 60% forest cover as the threshold for a park considered forested. We subsetted all park visitation data to include only those parks with >60% forest cover as determined by NLCD. Total visitation counts (both camping and day use) of this group of parks were summed per year. We set the dataset target as the maximum value in the dataset plus 10% of the range. The annual score was computed as the difference between the lower scoring bounds (minimum value in the data minus 10% of the range) and the target. This difference was then scaled from 0-1.
Data on forest bird counts by species were collected by Vermont Center for Ecostudies1 at forested locations throughout Vermont between 1989-2017. From these data, we computed a Living Planet Index (LPI) 2. We used a beta package for R, rlpi3, to compute the LPI for all species and birds. We used equal weighting among species and no sub-groupings. Only those Forest Bird Monitoring sites with a complete record were included: Cornwall Swamp, Dorset Bat Cave, Moose Bog, Roy Mt WMA, Shaw Mt, Sugar Hollow, The Cape, and Underhill State Park.
Shannon-Weiner Index (H’)
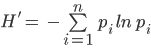
Where pi is the proportion of trees in the ith size class
Data on the pH of precipitation were accessed from the National Atmospheric Deposition Program (NADP)1. Data were collected from the Underhill, Vermont. We set a target for precipitation acidity of 5.6, based on a previously established value2. The annual score was computed as the difference between the lower scoring bounds (minimum value in the data minus 10% of the range) and the target value (5.6). This difference was then scaled between 0-1. Values above the target receive a 1.
Using MODIS remotely sensed phenology products, we selected Time Integrated Normalized Difference Vegetation Index (NDVI)1 as an assessment of the total length of the functional growing season. We used ArcDesktop (version 10.4) to clip images to the state of Vermont boundary2, and masked to limit only those pixels identified as forested (Deciduous (41), Evergreen (42), and Mixed (43), and Woody Wetlands (90) cover pixels), according to 2011 National Land Cover Dataset3. In each MODIS image, we excluded values of -1000 (unknown) and 1000 (water), then calculated the mean pixel value per image. We also computed the mean for each pixel over all image years and then computed the mean across pixels to establish the long-term mean of the dataset. We set the data target as the long-term mean and computed the annual score as the difference from this target. This difference was then scaled from 0-1.
Daily ozone data (ppm-hour) was accessed from the National Atmospheric Deposition Network (NADP) sites at Underhill (Proctor Maple Research Forest) and Bennington (Morse Airport), Vermont1. To compute an ozone exposure index, we selected the W126 standard2 because it is thought to be better representation of ozone injury to plants. Under this, Vermont’s ozone monitoring season runs April 1 to September 30 and growing hours are 8:00 am to 8:00 pm. We determined the minimum detection limit per site (here 0.005 for both sites over the entire record). We backfilled missing values with the the minimum value observed per year, restricted to the established monitoring season and growing hours. All months must have >75% completeness in daily records to be utilized. Data were transform following the equation: OZ*(1/(1+4403*EXP((OZ*(-126))))). A daily index value was calculated by summing the transformed values per day; these were then summed per month to compute a monthly index value. These monthly indices were multiplied by the ratio of collected and backfilled samples to total possible samples within the month. For each month, we computed a three-month maximum -- the current month plus the two preceding months (i.e., the 3-month maximum for June is the maximum of June, May and April). In Vermont, this results in 3-month maximum values for June, July, August and September. To compute the annual W126, we took the mean of the largest 3-month maximum over the current year and the previous two years. We set the target for ozone exposure at 7 ppm-hour3. The annual score was computed as a difference between 7 and the upper scoring bounds (maximum value in the dataset plus 10% of the range). This difference was scaled from 0-1.
Data on mercury deposition (µg/m2) were accessed from the National Atmospheric Deposition Program (NADP) Mercury Deposition Network (MDN) for sites at Underhill, Vermont1. Annual values are compute from weekly samples collected at the site. We set the target for mercury deposition to zero2. The annual score was computed as the difference between the target concentration of 0 µg/m2 and upper scoring bounds (maximum value in the data plus 10% of the range). This difference was then scaled between 0-1.
Data of mean minimum annual temperature (℉) for Vermont were gathered from NOAA National Centers for Environmental Information1. We set the target for the dataset as the mean minimum temperature from 1961-1990 based on the baseline set by the IPCC. Annual scores were computed as the deviation from the data target, scaled from 0-1.
Data of mean maximum annual temperature (℉) for Vermont were gathered from NOAA National Centers for Environmental Information1. We set the target for the dataset as the mean maximum temperature from 1961-1990 based on the baseline set by the IPCC. Annual scores were computed as the deviation from the data target, scaled from 0-1.
Data of annual total precipitation (inches) for Vermont were collected from NOAA National Centers for Environmental Information1. We set the target for the dataset as the total precipitation from 1961-1990 based on the baseline set by the IPCC. Annual scores were computed as the deviation from the data target, scaled from 0-1.
The total annual number of days with snow cover >1 inch in Vermont were collected from NOAA National Centers for Environmental Information1. We set the target for the dataset as the mean duration of snow cover from 1961-1990 based on the baseline set by the IPCC. Annual scores were computed as the deviation from the data target, scaled from 0-1.
NOAA National Centers for Environmental Information (NCEI) provides a robust Climate Extremes Index for the northeastern US1. NCEI computes the regional CEI based on a set of climate extreme indicators: (1) monthly maximum and minimum temperature, (2) daily precipitation, and (3) monthly Palmer Drought Severity Index (PDSI). The CEI is a combination of the proportion of the year and the area in the region that has experienced an extreme event for these three indices. NCEI has defined extremes as those CEI values that fall in the upper (or lower) tenth percentile of the local, period of record. Please refer to NCEI documentation for more details on calculations. Accordingly, a value of 0% for the CEI indicates that no portion of the year was subject to any of the extremes considered in the index. In contrast, a value of 100% indicates that the entire northeast region had extreme conditions throughout the year for each of the indicators. The long-term variation or change in the CEI represents the tendency for extremes of climate to either decrease, increase, or remain the same1. We set the target for the dataset as the long-term mean. Annual scores were computed as the deviation from the data target, scaled from 0-1.
Dought was assessed through the Standardized Precipitation Evapotranspiration Index (SPEI) for Vermont1. The SPEI more fully captures the effect of drought on plants than the Palmer Drought Severity Index, as the former includes the loss of water through evapotranspiration. We selected a six month SPEI value which spans from April-September to capture drought in the functional growing season. We set the target for the dataset as the mean duration of snow cover from 1961-1990 based on the baseline set by the IPCC. Annual scores were computed as the deviation from the data target, scaled from 0-1.
To quantify the damage caused by invasive insects and diseases, we use Insect and Disease Surveys (IDS), which are annual aerial surveys of forests conducted by the State of Vermont and the USDA Forest Service to map forest disturbance1. Here, we summed the total area mapped by pests that we could determine as invasive to Vermont. The current year is scored as the difference between the minimum and maximum (+10%) values in the record. Annual scores were computed as the deviation from the data target, scaled from 0-1.
On the overview page, you will see four categories: Structure, Condition, Services, and Stressors. Each of these metrics has a short description, and is a compilation of a number of pertinent datasets which can be explored further. For the four indicator categories and the datasets contained within, a value is given for the current status on a scale of 1 to 5; values closer to 5 indicate a more favorable condition or status. The colored circle adjacent to that value indicates the long-term trend. Red indicates that the long-term trend is a worsening of this condition, status, or function. Yellow indicates stable, and green indicates an improvement over time.
If you would like more information on an indicator category, click on it. You will be taken to the individual input datasets, which you can explore. Each of these has information on the dataset, the reason why it is important, our calculations of the score and trend, as well as a link to the data, and reference for more information. The dataset is also presented graphically allowing you to see the long-term trends.
FEMC staff developed the Forest Indicators Dashboard with guidance and input provided by expert professionals. Several dozen FEMC cooperators attended a working session at the FEMC Annual Meeting (9 December 2016) to facilitate the initial concept and design of the FID, as well as brainstorm potential long-term, pertinent datasets for inclusion. Once a proof-of-concept was developed, the FEMC gathered the following expert panel to provide a technical review of the FID (20 March 2018), which included determining the variable weightings of each dataset:
John Austin Jamey Fidel Mollie Flanigan Josh Halman Robbo Holleran Bennet Leon Aaron Moore Randy Morin Jared Nunery Jessica Savage Bruce Shields Steve Sinclair Jay Strand Keith Thompson Bob Zaino
We are thankful to all experts who provided input and feedback on the development of the FID.
The scores presented in the dashboard can change as new data is added to the individual long-term datasets. To enable users to link to snapshots that are stable over time, we provide a version history for the Indicator Dashboard. The date indicates when the new version of the dashboard was created.
Select a version: