
(This was originally written as a lab assignment, which explains the instructions. To make this document useful to others, I'll describe the background briefly. This example is based on a study by Foa, Rothbaum, Riggs, and Murdock (1991) in the Journal of Counseling and Clinical Psychology. The subjects were 45 rape victims who were randomly assigned to one of four groups. The four groups were 1) Stress Inoculation Therapy (SIT) in which subjects were taught a variety of coping skills; 2) Prolonged Exposure (PE) in which subjects went over the rape in their mind repeatedly for seven sessions; 3) Supportive Counseling (SC) which was a standard therapy control group; and 4) a Waiting List (WL) control.
In the actually study pre- and post-treatment measures were taken on a number of variables. For our purposes we will only look at post-treatment data on PTSD Severity, which was the total number of symptoms endorsed by the subject.
1. Log onto your computer create two files. The data and SAS program for these files are attached to the end of this document. I have used a SAS program, but there is no reason why you can't readily adapt this to whatever program you have available.
2. Then run the SAS program to get the analysis of variance, checking the two output files to make sure everything looks fine. What do these results tell you about the reasonableness of the assumptions behind the analysis of variance? (They won't tell you everything you need to know, but they will tell you something.)
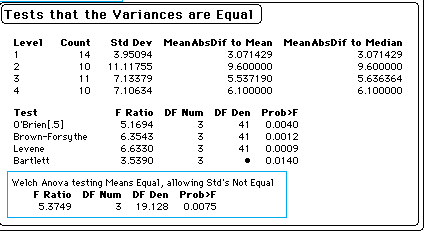
There are not enough data points to say anything meaningful about the normality assumptions behind anova. However we can look at the group variances. (The statistics can be found in the JMP printout below, or in the SAS printout, which is not shown.) The variances range from 15.60 to 123.65. This would give me some concern about the homogeneity of variance assumptions. For further tests on this assumption, see p. 197f of the Methods book (4th edition), and for alternative ways of dealing with heterogeneity, see the sections on violations of assumptions (pp 321-323) and transformations (pp 3023-329) in Chapter 11. A portion of the printout from JMP testing for heterogeneity of variance reveals that the variances are indeed significantly different, but the group differences that we will see in the SAS output below are also significant if we use Welch's adjustment.
Subsequent analyses ignore the problem of heterogeneity of variance, but don't be mislead. The problem is not a trivial one. When we begin to work with multiple comparison techniques in a serious way, I'll come back to this example and show how we might deal with heterogeneity in comparing groups. For now, however, we will follow the standard analysis.

3. Now Remove the Proc Sort and Proc Means procedures, because they are not necessary in what follows and just increase the amount of printout. They were just included so that you could see how they work. If the data had not already been entered in increasing order of group membership, the Proc Sort procedure would have been absolutely necessary before Proc Means, because Proc Means contained a "BY" statement.
4. The standard textbook way to write the analysis of variance summary table would be as follows:
Source df SS MS F Between groups 3 507.84 169.28 3.05 * Error 41 2278.75 55.58 Total 44 2786.59
Find each of these terms in your printout. How are they labelled differently?
The SAS printout follows:
General Linear Models Procedure
Class Level Information
Class Levels Values
GROUP 4 1 2 3 4
Number of observations in data set = 45
General Linear Models Procedure
Sum of Mean
Source DF Squares Square F Value Pr of F
Model 3 507.84011544 169.28003848 3.05 0.0381
Error 41 2278.73766234 55.57896737
Corrected Total 44 2786.57777778
R-Square C.V. Root MSE SYMPTOMS Mean
0.182245 47.72132 7.4551303 15.6222
Source DF Type III SS Mean Square F Value Pr of F
GROUP 3 507.84011544 169.28003848 3.05 0.0381
I assume that you can find each of the effects in the printout. I would point out a couple of things. In the first place, for the OVERALL analysis, which comes first, the Between groups effect that you are looking for is labelled Model. That term actually covers all of the independent variables in this design, but since there is only one variable, the Between groups term and the Model term are equivalent. If you look further down you will see the Group effect. This is a partition of the Model effect, but, again because there is only one independent variable, they are the same.
Notice that the second part of the printout contains the label Type III SS. In complex designs there are different ways of computing the sum of squares for effects when there are unequal n's. Generally, the Type III SS are the ones you want. In a oneway design, the alternative approaches reduce to the same thing.
5. In Chapter 11 I defined two statistics for the magnitude of effect. The calculations are shown below for eta-squared:
![]()
and for omega-squared
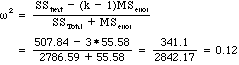
Calculate these two statistics from the results that SAS produced. (Eta-squared actually is given on the printout. Can you find it?)
Answer: It is the R-square term.
6. Make some predictions from what you know about the Foa et al. study in terms of which groups will be different from which other groups. Here we are about to go beyond what is covered in Chapter 11, but I want you to have some experience before we get to Chapter 12.
I would predict that each of the main intervention groups would differ from each of the control groups. Because of the small sample size, it is quite possible that I would not find a significant difference here. I would also hope to show that the two intervention groups differed from each other, although here I have even less power. In this experiment I would actually be happy if the SIT and Waiting List control were different.
7. One way to compare groups following an analysis of variance is to run a simple t test between means. Suppose that you wanted to compare the Prolonged exposure group (Group 2) with the Supportive Counselling group (Group 3). We can compare those groups using
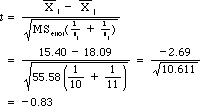
Run this test to compare the two groups, doing the calculations with a calculator. (I have since filled in the formula and solved for t above.)
Because MSerror is based on 41 degrees of freedom, we would use those df for our t . This would give a critical value of approximately 2.021, which far exceeds our calculated value. We would not reject H0 and would conclude that there is no reason to decide that Prolonged Exposure is any better as a treatment than standard Supportive Counseling.
8. Replace the "Means Group;" line in GLM with the following to calculate multiple comparison tests.
Means Group /LSD Bon SNK Tukey;
These results are not immediately obvious in terms of interpretation. What sense can you make of them? (It will take a bit of thought, but if you compare your hand-calculated stuff in #5 with the answers here, it should make some sense.
These results follow, but only for pairwise t tests between groups (otherwise known as the Least Significant Difference test). This solution is somewhat different from any that you have seen before. The rest of the tests are, in part, self-evident. The differences between them will be explained in a future assignment.
In the past we have taken the obtained statistics and solved for t . Any value of t that exceeded the critical value in the table was considered to be significant. Here we do it backward. We already know from the previous calculation that the critical value that we need is 2.02. Notice this value below. We also know Mserror and the sample sizes, so we can easily compute the denominator for t . Knowing the denominator and the critical value, we can compute the minimum distance between means that would just barely be significant. Any difference larger than that would certainly be significant. This minimum distance is shown in the following printout as 6.4084. If you substitute that difference in the formula and solve for t , you will see that the result is 2.02, our critical value.
The rest of the printout is also unusual. You will see that the means are listed in numerical order, and that the letters A and B have been written down the side. The rule is that all means that are linked by the same letter are not significantly different. Thus Groups 2, 3, and 4 are all linked by an A, and thus don't differ. Groups 4 and 1, and Groups 3 and 1 don't share a common letter, and hence they are significantly different. But Groups 1 and 2 share a B, and are thus not different. Another way of saying this is to say that the mean of Group 1 is more than 6.4 points away from the means of Groups 3 and 4, but that all other pairs are closer than 6.4.
General Linear Models Procedure
T tests (LSD) for variable: SYMPTOMS
NOTE: This test controls the type I comparisonwise error rate not the
experimentwise error rate.
Alpha= 0.05 df= 41 MSE= 55.57897
Critical Value of T= 2.02
Least Significant Difference= 6.4084
WARNING: Cell sizes are not equal.
Harmonic Mean of cell sizes= 11.03943
Means with the same letter are not significantly different.
T Grouping Mean N GROUP
A 19.500 10 4
A
A 18.091 11 3
A
B A 15.400 10 2
B
B 11.071 14 1
From this analysis we would conclude that both Stress Inoculation Therapy and Prolonged Exposure therapy show significantly better results than simply leaving the patients on a waiting list, but that they are not significantly different from a therapy control group (the Supportive Counseling condition). It should be kept in mind that this analysis is somewhat simpler than the design used by Foa et al., although the conclusions essentially agree with theirs.
I commented earlier on the heterogeneity of variance exhibited by these groups. The results obtained from the Welch test, however, tell us that these differences are sustained when we take a more appropriate approach to variance inequality.
Foa, E. B., Rothbaum, B. O., Riggs, D. S., & Murdock, T. B. Treatment of posttraumatic stress disorder in rape victims: A comparison between cognitive-behavioral procedures and counseling. Journal of Consulting and Clinical Psychology, 59, 715-723.
First column = ID, Second = Group, Third = Symptom Score
| ID | Group | Score |
| 1 | 1 | 3 |
| 2 | 1 | 13 |
| 3 | 1 | 13 |
| 4 | 1 | 8 |
| 5 | 1 | 11 |
| 6 | 1 | 9 |
| 7 | 1 | 12 |
| 8 | 1 | 7 |
| 9 | 1 | 16 |
| 10 | 1 | 15 |
| 11 | 1 | 18 |
| 12 | 1 | 12 |
| 13 | 1 | 8 |
| 14 | 1 | 10 |
| 15 | 2 | 18 |
| 16 | 2 | 6 |
| 17 | 2 | 21 |
| 18 | 2 | 34 |
| 19 | 2 | 26 |
| 20 | 2 | 11 |
| 21 | 2 | 2 |
| 22 | 2 | 5 |
| 23 | 2 | 5 |
| 24 | 2 | 26 |
| 25 | 3 | 24 |
| 26 | 3 | 14 |
| 27 | 3 | 21 |
| 28 | 3 | 5 |
| 29 | 3 | 17 |
| 30 | 3 | 17 |
| 31 | 3 | 23 |
| 32 | 3 | 19 |
| 33 | 3 | 7 |
| 34 | 3 | 27 |
| 35 | 3 | 25 |
| 36 | 4 | 12 |
| 37 | 4 | 30 |
| 38 | 4 | 27 |
| 39 | 4 | 20 |
| 40 | 4 | 17 |
| 41 | 4 | 23 |
| 42 | 4 | 13 |
| 43 | 4 | 28 |
| 44 | 4 | 12 |
| 45 | 4 | 13 |
*****************************
For further information I recommend that you go back to the original
article. I plan to put a repeated measures example here based on the same study, but that
will take a while.
![]()
![]()
 Return to
Dave Howell's Statistical Home Page
Return to
Dave Howell's Statistical Home Page
Send mail to: David.Howell@uvm.edu)
dch
Last revised 3/6/2009