


Just as with other problems, there is a difference between randomization testing and bootstrap estimation. In the former, we are primarily interested in hypothesis testing, whereas the latter is primarily concerned with parameter estimation. We will come to bootstrapping later, but this page is primarily devoted to randomization. But let's not leave the distinction too quickly.
When we look at the bootstrap approach to correlation, we will see a procedure in which a very large number of resamples are drawn pairwise from a pseudo-population consisting of the observations in the original sample. The data consisted of pairs of observations on each experimental unit. Units are drawn, with replacement, from the pseudo-population, and a correlation coefficient is computed. After this procedure has been repeated B > 1000 times, the resulting correlation coefficients form the sampling distribution of r. We will then be able to set confidence limits on ρ using this sampling distribution. As I said earlier, bootstrapping focuses primarily on parameter estimation, whereas randomization tests focus primarily on hypothesis testing.
When we apply randomization tests to bivariate data, our primarily goal is to test a null hypothesis, usually that ρ = 0. We do this by holding one variable (e.g. X) constant, and permuting the other variable (Y) against it. Because, under this scheme, each Xi is randomly paired with a value of Y, the expected value of the correlation is 0. By repeating this process a large number of times, we can build up the sampling distribution of r for that situation in which the true value of ρ is 0.0. We can either create confidence limits on ρ or we can increment a counter to record the number of times a correlation coefficient from a bivariate population where ρ exceeds the obtained sample correlation (for either a one- or a two-tailed test.)
Elsewhere I have discussed a study by Katz et al. (1990) that dealt with asking students to answer SAT-type questions without having read the passage on which those questions were based. (For non-U.S. students, the SAT is a standardized exam commonly used in university admissions.) The authors looked to see how performance on such items correlated with the SAT scores those students had when they applied to college. It was expected that those students who had the skill to isolate and reject unreasonable answers, even when they couldn't know the correct answer, would also be students who would have done well on the SAT taken sometime before they came to college.
The data for that study follow. The data have been created to have the same correlation and descriptive statistics as the data that Katz et al. collected.
Score 58 48 48 41 34 43 38 53 41 60 55 44 43 49 SAT 590 590 580 490 550 580 550 700 560 690 800 600 650 580 Score 47 33 47 40 46 53 40 45 39 47 50 53 46 53 SAT 660 590 600 540 610 580 620 600 560 560 570 630 510 620
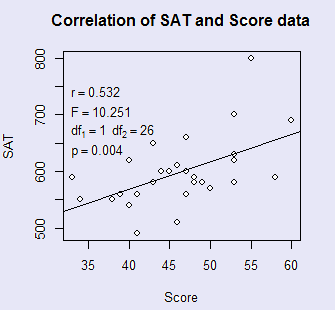
When we plot the two variables against each other we obtained the plot shown at the right. Notice that the correlation is .532, and the probability is given as .004. That probability, remember, is thre result of a parametric t or F test.
The randomization test is shown below. (It looks much better in Firefox. Internet Explorer makes it look weird.) The R code is shown at the end of this document and can be can be downloaded at randomCorrR.r
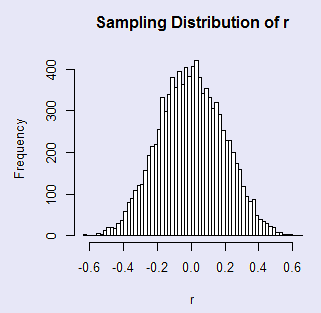
There were 21 random samples with a correlation greater than the obtained correlation This gives a probability of 0.0021
In this figure you can see that the correlation obtained by Katz et al. (1990) on the original data was .532. You can also see that the sampling distribution of r under randomization is symmetrical around 0.0, and that 21 of the 10000 randomizations exceeded +.532. This gives us a probability under the null of .0021, which will certainly allow us to reject the null hypothesis. This is a two-tailed test, and, because the distribution is symmetric for ρ >= 0, you will not go far wrong if you cut the probability in half for a one-tailed test. (These obtained probabilities usually vary slightly from one set of permutations to another, but the fact that I set the random seed equal to a specific value means that the randomization process always starts with that value and always gives the same result.) The code for this analysis follows:
# Resampling for correlation Score <- c( 58, 48, 48, 41, 34, 43, 38, 53, 41, 60, 55, 44, 43, 49, 47, 33, 47, 40, 46, 53, 40, 45, 39, 47, 50, 53, 46, 53) SAT <- c(590,590,580,490,550,580,550,700,560,690,800,600,650,580, 660,590,600,540,610,580,620,600,560,560,570,630,510,620) # First we will use standard parametric statistics to evaluate the correlation. reg <- lm(SAT ~ Score) # I need this to draw the regression line on the plot. cor <- round(cor(SAT, Score), digits = 3) # See resulting answers on plot. F <- round(summary(reg)$fstatistic[1], digits = 3) df1 <- summary(reg)$fstatistic[2] df2 <- summary(reg)$fstatistic[3] p <- round(1-pf(10.25,1,26), digits = 3) par(mfrow = c(2,2)) plot(SAT ~ Score, main = "Correlation of SAT and Score data") abline(reg$coef, lty=1) legend(30,770,bquote(paste(r == .(cor))), bty = "n") legend(30 , 735, bquote(paste(F == .(F))), bty = "n") legend(30,700,bquote(paste(df[1] == .(df1))), bty = "n") legend(35,700,bquote(paste(df[2] == .(df2))), bty = "n") legend(30, 665, bquote(paste(p == .(p))), bty = "n") # Now we will use a randomization test. nreps = 10000 # Note: 10,000 replications N <- length(SAT) r <- numeric(nreps) counter = 0 set.seed <- 1086 #This will force each run to come to the same result. for (i in 1:nreps) { randScore <- sample(Score, N, replace = FALSE) r[i] <- cor(SAT, randScore) if(r[i] >= cor) counter = counter + 1 } hist(r, main = "Sampling Distribution of r", breaks = 50) cat("There were ",counter," random samples with a correlation greater than the obtained correlation \n") cat("This gives a probability of ",counter/nreps,'\n \n') # Now we will look at the same data using Kendall's nonparametric statistic. #Kendall's tau library(Kendall) Alc <- c(4.02, 4.52, 4.79, 4.89, 5.27, 5.63, 5.89, 6.08, 6.13, 6.19, 6.47) Tob <- c(4.56, 2.92, 2.71, 3.34, 3.53, 3.47, 3.20, 4.51, 3.76, 3.77, 4.03) print(cor.test(Alc,Tob,alternative = "two.sided", method = "kendall", ,exact = TRUE)) # Kendall's rank correlation tau # #data: Alc and Tob #T = 37, p-value = 0.1646 #alternative hypothesis: true tau is not equal to 0 #sample estimates: # tau #0.3454545 # Kendall's p value is not even close.
This is a good place to again make a point that was made earlier about the difference between bootstrapping and randomization procedures. (Yeah, I know. I am beating a dead horse. This will be the last time--I hope.) I make it here because the difference between the two approaches to correlation is so clear. (This section was written in an earlier version where I discussed bootstrapping before randomization. It should be possible to follow this even though we have not yet discussed bootstrapping in any detail.)
When we bootstrap for correlations, we keep Xi and Yi pairs together, and randomly sample pairs of scores with replacement. That means that if one pair is 45 and 360, we will always have 45 and 360 occur together, or neither of them will occur. And because we are sampling with replacement, it is quite possible that the pair, (45, 360), will occur more than once in our resample. What this means is that the expectation of the correlation between X and Y for any resampling will be the correlation in the original data. It certainly won't always be the same, but the best guess (the expectation) is that it will be the original correlation.
When we use a randomization approach, we permute the Y values, while holding the X values constant--or vice versa. For example, if the original data were
45 53 73 80
22 30 29 38
then three of our resamples might be
|
45 53 73 80 |
45 53 73 80 |
45 53 73 80 |
Notice how the top row always stays in the same order, while the bottom row is permuted randomly. This means that the expected value of the correlation between X and Y will be 0.00, not the correlation in the original sample.
This helps to explain why bootstrapping focuses on confidence limits around ρ whereas the randomization procedure focuses on confidence limits around 0.00 (or counts the number of bootstrapped correlations more extreme than r). I see no way that you could apply a permutation procedure with the intent of having the results have an expectation of ρ. Similarly, I don't see how you would set up the bootstrap to be centered on 0.00 (unless you bootstrapped (r* - r), which is an interesting possibility, and one that I will think about).
Katz, S., Lautenschlager, G. J., Blackburn, A. B., & Harris, F. H. (1990) Answering reading comprehension items without passages on the SAT. Psychological Science, 1, 122-127.

 dch:
dch: