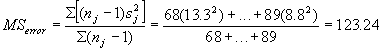
This is my version of the answers to the second question in this lab. I haven't checked my work sufficiently, but these look like reasonable answers.
Problem #2 from Lab of 1/22/98
This problem first called for a Tukey test. In order to run a Tukey test you must know
The means
The cell variances
The cell sizes (nI)
MSerror can be found as
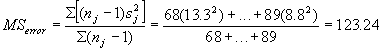
We then create a table with means on the rows and columns, arranged in increasing order.
|
A |
C |
PC |
P |
||||
|
Group |
Means |
13.7 |
16.6 |
24.8 |
28.8 |
r |
Wr |
|
A |
13.7 |
-- |
2.9 |
11.1* |
15.1* |
4 |
6.65 |
|
C |
16.6 |
-- |
-- |
8.2* |
12.2* |
3 |
6.65 |
|
PC |
24.8 |
-- | -- |
-- |
4.0 |
2 |
6.65 |
|
P |
28.8 |
-- | -- | -- | -- |
1 |
6.65 |
![]()
I will first do this using a harmonic mean for n, and then Iíll do the heavy-duty Games-Howell procedure with separate error terms.
For Tukey, the critical value of q is always taken at its maximum, which is the number of conditions. In this case it is 4.
![]()
All difference greater than 6.65 will be significant, and these differences are reflected in the pattern of asterisks in the table.
We can see that the Action group is significantly different from the Preparation and Precontemplative groups, and the Contemplation group is also different from both of those groups.
This leaves us with the following pattern
A C PC P
*******
******
Now comes the hard part. I want to use the Games-Howell procedure to get around the problem with the unequal variances and unequal sample sizes.
That procedure uses a different critical value for each cell, based on the following formula: (I can't imagine an instructor would give such an assignment.)
First I will make a table of df, making liberal use of Excel to simplify my calculations.
When I calculate these in Excel I get the following, rounded to 2 decimal places:
|
A |
C |
PC | |
|
A |
---- |
---- |
---- |
|
C |
121.57 |
---- |
---- |
|
PC |
137.80 |
97.35 |
---- |
|
P |
231.07 |
111.69 |
109.36 |
The I have to make up a table of q values given the df` values I calculated. Since I am trying to apply this to Tukeyís test, I will let r = k = 4 throughout. (At least something is simpler.)
Values of q.05(4,df`) for each comparison
|
A |
C |
PC | |
|
A |
---- |
---- |
---- |
|
C |
3.69 |
---- |
---- |
|
PC |
3.68 |
3.72 |
---- |
|
P |
3.65 |
3.70 |
3.68 |
I got these values out of the book, but I had to guess at them. Itís pretty hard to interpolate between something and infinity. I doubt that this will make much difference anyway.
The following formula is the one I want. The first unknown is given by the previous table, but I havenít yet calculated the secondóthe square root of the sum of the variances divided by their sample size. Back to Excel, and reported in the table below.
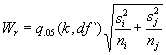
Variances divided by sample sizeóthe square root thereof
|
A |
C |
PC | |
|
A |
---- |
---- |
---- |
|
C |
1.261 |
---- |
---- |
|
PC |
1.850 |
1.815 |
---- |
|
P |
1.354 |
1.305 |
1.881 |
Now I just have to multiply the corresponding cells to get Wr.
Wr = critical differences between means
|
A |
C |
PC | |
|
A |
---- |
---- |
---- |
|
C |
4.653 |
---- |
---- |
|
PC |
6.808 |
6.752 |
---- |
|
P |
4.942 |
4.828 |
6.922 |
Finally, I show the actual mean differences below, with asterisks showing the pattern of differences. I know the table is reversed, but itís getting late and the matrix is symmetric, so it doesnít matter.
|
A |
C |
PC |
P | ||
|
Group |
Means |
13.7 |
16.6 |
24.8 |
28.8 |
|
A |
13.7 |
-- |
2.9 |
11.1* |
15.1* |
|
C |
16.6 |
-- |
-- |
8.2* |
12.2* |
|
PC |
24.8 |
-- | -- |
-- |
4.0 |
|
P |
28.8 |
-- | -- | -- | -- |
The one difference from the standard Tukey test is shown by the double asterisk on C versus PC. I would think that in general we would lose some differences because we lose df for each comparison when we do it this way. But here we were comparing two groups, once of which had a small variance, and that compensated for the loss in df.
Now I will look at your papers, and if they donít agree with mine Iíll get mad and blame you for the error. This assignment was too long.
dch