

![]()
![]()
This web page is a step by step demonstration of using NORM (give ref.) to handle multiple imputation. It is deliberately not a theoretical discussion. The first draft was a big mess, and I hope that this draft is just a little mess.
The data file is named Cancer.dat and contains the following variables related to child behavior problems among kids who have a parent with cancer. Most of the variables in this example (a truncated data set) relate to the parent (patient) with cancer. The variable names are, in order, SexP (sex parent), deptp (parent's depression T scorea), anxtp (parent's anxiety T score), gsitp (parent's global symptom index T score), depts, anxts, gsits (same variables for spouse), sexchild, totbpt (total behavior problem T score for child). These are a subset of a larger dataset, and the analysis itself has no particular meaning. I just needed a bunch of data and I grabbed some variables. We will assume that I want to predict the child's behavior problem T score as a function of the patient variables. I no longer recall whether the missing values were actually missing or whether I deleted a bunch of values to create an example.
The first few cases are shown below. Notice that variable names are NOT included in the first line. Missing data are indicated by -9. NORM only allows a few codes for missing, and -9 is one of them, but "." is not.
2 50 52 52 44 41 42 -9 -9 1 65 55 57 73 68 71 1 60 1 57 67 61 67 63 65 2 45 2 61 64 57 60 59 62 1 48 2 61 52 57 44 50 50 1 58 1 53 55 53 70 70 69 -9 -9 2 64 59 60 -9 -9 -9 -9 -9 1 53 50 50 42 38 33 2 52 2 42 38 39 44 41 45 -9 -9 2 61 61 55 44 50 42 1 51 1 44 50 42 42 38 43 -9 -9 2 57 55 51 44 41 35 -9 -9 -9 -9 -9 -9 57 52 57 2 65 2 70 59 66 -9 -9 -9 1 61 2 57 61 52 53 59 53 2 49
To enter the data start NORM.exe and select File/New Session. Then select the file, which I called CancerNorm.
The Help files are excellent (mostly), and I recommend that you read them carefully.
The first step that you want to carry out is to run the EM algorith. This estimates means, variances, and covariances in the data. First a bit of theory. EM looks at the data and comes up with estimates of means, variances, and covariances. Then it uses those values to estimate missing values. But when we add in those missing values, we come up with new estimates of means, variances, and covariances. So we again estimate missing values based on those estimates.
This, in turn, changes our data and thus our next estimates. But for a reasonably sized sample, this process will eventually converge on a stable set of estimates. We stop at that point.
Next you want Data Augmentation. Data Augmentation (DA) is the process that does most of the work for you. It takes estimates of population means, variances, and covariances, either by taking the output of EM or by recreating them itself. Again we need a tiny bit of theory. Using the means, variances, and covariances, DA first estimates missing data. But then it uses a Baysian approach to create a likely distribution of the parameter values. For example, if the mean with the adjusted data comes out to be 52, it is reasonable to expect that the population mean falls somewhere around 52. But instead of declaring it to be 52, it draws at estimate at random from the likely distribution of means. This is a Baysian estimate because we essentially say what would the distribution of possible means really look like given the obtained sample mean. To oversimplify, think of calculating a sample mean on the basis of data. Then think of creating a confidence limit on the population mean given that sample mean. Suppose that the CI is 48 - 56. Then think of randomly drawing an estimate of mu from the interval 48-56, and then continuing with an interative process. This is greatly oversimplified, but it does contain the basic idea. And, remember, we are going to continue this process until it converges.
To run DA,you could take the defaults, by clicking on the Data Augmentation tab. However, we need to do a little more because we want to create several possible sets of data. In other words, we want to run DA and generate a set of data. Then we want to run DA over again and create another set. In all we might create 5 sets of data, each of which is a reasonable sample of complete data with missing values replaced by estimated values.
Rather than run the whole program 5 times, what we do is to run it, for example, through 1000 iterations. In other words, we will go through the process 1000 times, each time estimating data, then estimating parameters, then reestsimating data, etc. But after we have done it 200 times, we will write out that data set and then keep going. After 400 iterations we will write out another data set, and keep going. After the 1000th iterations we will write out the 5th data set.
Now you have 5 complete sets of data, each of which is a pretty good guess at what the complete data would look like if we had it. We would HOPE that whichever data set we used we would come to roughly the same statistical conclusions. For example, if our analysis were multiple regression, we would hope, and expect, that each set would give us pretty much the same regression equation. And if that is true, it is probably reasonable to guess that the average of those five regression equations would be even better. For example, we would average the five estimates of the intercepts, the five estimates of b1, etc. We won't do exactly this, but it is close.
But you might ask why I chose 1000, 200, and 5. Well, the 5 replications was chosen because Rubin (1987) said that 3 - 5 seemed like a nice number. Well, it was a bit more sophisticated than that, but I'm not going there. So let m = 5. But how many interations before we print out the first set of imputed data? Schafer and Olsen (1989) suggest that a good starting point is a number larger than the number of iterations that EM took to converge, which, for our data, was 56. So I could have used 60, but k = 200 seemed nice. Actually it was overkill, but that won't hurt anything, and you are not going to fall asleep waiting for the process to go on for k*m = 1000 times. It will take a couple of seconds.
This is the point at which we put NORM aside for the moment and pull out SPSS or something similar. We simply take our m = 5 datasets, read them each into SPSS, run our 5 multiple regressions, record the necessary information, and turn off SPSS. In fact, it would be much nicer if you wanted to use SAS because you can tell SAS to save the 5 sets of coefficients, along with the corresponding covariances, and then have SAS put them altogether. I'll write up a similar, but much shorter, document about SAS when I get home and load SAS on my machine.
I suggested above that you are basically just going to average the coefficients from the 5 regressions--or similar stuff from 5 analyses of variance, logistic regressions, chi-square contingency table analyses, or whatever. Well, that is sort of true. In fact for the actual coefficients that is exactly true. But we also want to take variability into account. Whenever you run a single multiple regression you know that you have a standard error associated with bi<.sub>. Square that to get a variance. But you also know that from one of the 5 analyses to another you are also going to have variability. We want to combine the within-analysis variance and the between-analysis variance and use that to test the significance of our mean coefficient. I know how to do this by hand, but I'm not really clear on how to have NORM handle it, although it will. The nice thing about SAS is that I know how to set up the whole thing. But what follows is the hand solution taken from Schafer & Olsen (1998).
The table that follows contains the results of 5 imputations with the cancer data.
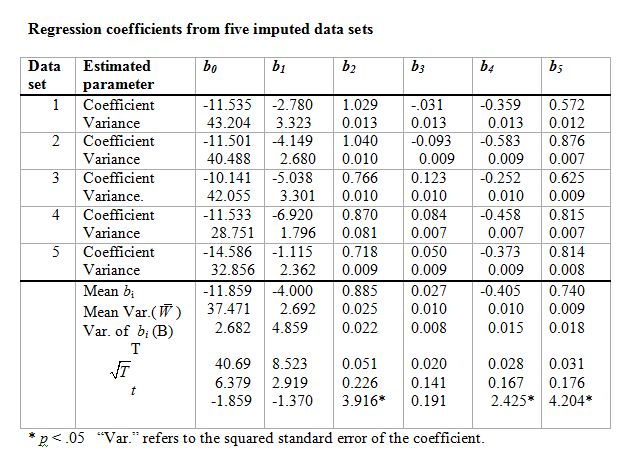
Thus the regression equation for the first set of data would be
Y = -11.535 -2,7831 + 1.0292 -0.0313 -0.3594 +0.5725.
The standard error of b1, for example, was 1.823, so its square (the variance) is 3.323, which you see in the table.
Notice that I have taken the means of the six bi. I have also taken the mean of the variances. Then I took the variance of the bi, shown in the third line at the bottom. Now I need to combine these two variances. This is calculated as
T = mean variance within (U) + (1 + 1/m)*variance of the bi.
For b1 this is 2.692 + (1+1/5)*4.859 = 8.523.
The square root of this is 2.919, which is our estimate of the standard error of the estimated b1 = -4.000. If we divide -4.000 by 2.919 we get -1.370, which is a t statistic on that coefficient. So that variable does not contribute significantly to the regression.
You will note that I used multiple regression here. If I had used an analysis of variance on these data I would have run 5 Anovas and done similar averaging. I haven't really thought through what that would come out to, but it shouldn't be too difficult. I suspect that I would average the MSbetween, average the MSwithin, take the variance of the SSbetween, and combine like I did above.
I can work this out a bit better when I get SAS going. More later.