Mixed Models
This section provides an overview of a likelihood-based approach to
general linear mixed models.
Matrix Notation
Suppose that you observe n data points y1, ... , yn and that you
want to explain them using n values for each of p explanatory
variables x11, ... , x1p, x21, ... , x2p, ... , xn1, ... , xnp. The xij
values may be either regression-type continuous variables or dummy
variables indicating class membership. The standard linear model for
this setup is

where 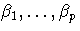 are unknown fixed-effects
parameters to be estimated and
are unknown fixed-effects
parameters to be estimated and 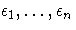 are
unknown independent and identically distributed normal (Gaussian)
random variables with mean 0 and variance
are
unknown independent and identically distributed normal (Gaussian)
random variables with mean 0 and variance 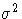 .
.The preceding equations can be written simultaneously using
vectors and a matrix, as follows:
![[y_1 \ y_2 \ \vdots \ y_n ]
=
[x_{11} & x_{12} & ... & x_{1p} \ x_{21} & x_{...
...beta_2 \ \vdots \ \beta_p ]
+
[\epsilon_1 \ \epsilon_2 \ \vdots \ \epsilon_n ]](Mixed-Model-Basics_files/mixeq152.gif)
For convenience, simplicity, and extendibility, this
entire system is written as
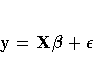
where y denotes the vector of observed yi's, X is the
known matrix of xij's, 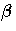 is the unknown fixed-effects
parameter vector, and
is the unknown fixed-effects
parameter vector, and 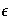 is the unobserved vector of
independent and identically distributed Gaussian random errors.
is the unobserved vector of
independent and identically distributed Gaussian random errors.
Formulation of the Mixed Model
The previous general linear model is certainly a useful
one (Searle 1971), and it is the one fitted by the GLM procedure.
However, many times the distributional assumption about 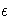 is too restrictive. The mixed model extends the general linear
model by allowing a more flexible specification of the covariance
matrix of
is too restrictive. The mixed model extends the general linear
model by allowing a more flexible specification of the covariance
matrix of 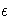 . In other words, it allows for both
correlation and heterogeneous variances, although you still assume
normality.
. In other words, it allows for both
correlation and heterogeneous variances, although you still assume
normality.
The mixed model is written as
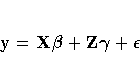
where everything is the same as in the general linear model except
for the addition of the known design matrix, Z, and the vector
of unknown random-effects parameters, 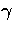 . The matrix Z can
contain either continuous or dummy variables, just like X. The
name mixed model comes from the fact that the model contains
both fixed-effects parameters,
. The matrix Z can
contain either continuous or dummy variables, just like X. The
name mixed model comes from the fact that the model contains
both fixed-effects parameters, 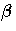 , and random-effects
parameters,
, and random-effects
parameters, 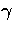 . Refer to Henderson (1990) and Searle,
Casella, and McCulloch (1992) for historical developments of the
mixed model.
. Refer to Henderson (1990) and Searle,
Casella, and McCulloch (1992) for historical developments of the
mixed model.
A key assumption in the foregoing analysis is that 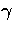 and
and
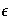 are normally distributed with
are normally distributed with
![E[
{\gamma}\ {\epsilon}]
& = & [0 \ 0
] \ {Var}[
{\gamma}\ {\epsilon}]
& = & [G& 0 \ 0 & R
]](Mixed-Model-Basics_files/mixeq154.gif)
The variance of y is, therefore, V = ZGZ' + R. You can
model V by setting up the random-effects design matrix Z and
by specifying covariance structures for G and R.
Note that this is a general specification of the mixed model.
A simple random effects are a special case of the general
specification with Z containing dummy variables, G
containing variance components in a diagonal structure, and 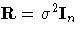 , where In denotes the n ×n identity
matrix.
, where In denotes the n ×n identity
matrix.
The general linear model is a further special case with
Z = 0 and 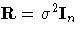 .
.
Copyright © 1999 by SAS Institute Inc., Cary, NC, USA. All rights reserved.


![[y_1 \ y_2 \ \vdots \ y_n ]
=
[x_{11} & x_{12} & ... & x_{1p} \ x_{21} & x_{...
...beta_2 \ \vdots \ \beta_p ]
+
[\epsilon_1 \ \epsilon_2 \ \vdots \ \epsilon_n ]](Mixed-Model-Basics_files/mixeq152.gif)
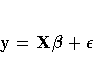
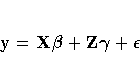
![]() and
and
![]() are normally distributed with
are normally distributed with
![E[
{\gamma}\ {\epsilon}]
& = & [0 \ 0
] \ {Var}[
{\gamma}\ {\epsilon}]
& = & [G& 0 \ 0 & R
]](Mixed-Model-Basics_files/mixeq154.gif)
![]() , where In denotes the n ×n identity
matrix.
, where In denotes the n ×n identity
matrix.
![]() .
.