Economics 172
Spring 2006
Due Monday March 13
Chapter 7
Questions 1, 5, 10, 16, 17
1. The fixed costs of Andre’s airplane is the cost of the plane itself. The fixed costs don’t vary with output. The total cost of flying is the cost of fuel and
labor and that goes up the more you use the plane. It’s not true that the more you fly it, the
more economic sense it makes. Flying to
5. When you spend more time on one question,
your marginal productivity falls. You
should allocate your time so that the additional points you get per minute
spent on the problem is equal to the additional points you get per minute spent
working on the second problem.
10. A 25%
government subsidy is a reverse tax. It
makes labor cheaper—a firm can get a given worker at a 25% discount. The firm will use more labor and less
capital.
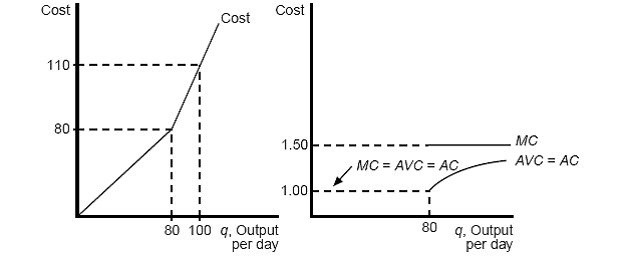
16. The firm’s cost function for output levels of 80 or less is C=q. If q=20, C=20 since it takes Gail 2 hours to
proeuce 20 floral arrangements. The AC
is C/q = $1. AVC = 1 as well, since
there is no
fixed cost given. It costs the firm $1 to produce one more unit of output so MC
= $1.
For output levels
greater than 80, C = 80 + 1.5(q-80) = 80 + 1.5q – 120 = 1.5q-40 since there is an $80 cost
to produce the first 80, then each additional arrangement after 80 costs
$1.50. If Gail produces 100 arrangments,
it takes her 10 hours and it costs the firm $80 + $30. The average cost for all output over 80 is C/q = 1.5-40/q, which is also AVC (after
q=80). Marginal cost is also 1.5q
17. You are given C = F + 10q – bq2 +
q3 and b>0.
a. For what values of b is C positive?
C > 0 when F +
10q – bq2 + q3 >0
So – bq2 > -F – 10q - q3
Multiply by
-1 bq2 < F + 10q + q3
Divide by q2 : C is
positive when b < F/ q2 +
10/q +q
That is true for
AC and MC as well as C (If total cost is positive, average and marginal costs
must be as well)
The AC curve is
C/q = F/q + 10 – bq + q2
which is U shaped.
b. MC = AC
MC = AVC: AVC = 10 – bq + q2
AVC = + 10 – bq +
q2
So MC = AVC where 10 – 2bq
+3q2 = 10 – bq + q2
c. Minimize AVC by taking the derivative of AC with respect to Q dAVC/dq = –b +2q = 0
so 2q = b
1.a.When the
Since the
government could hire workers (soldiers) at a wage lower than their opportunity
cost, the true cost to society of military spending was understated. If a 22 year old could be earning $20,000 and
year and the military paid $7,000, then the true cost of hiring the soldier is
$20,000, which understates the monetary cost by $13,000.
b. What does your answer imply about comparing the cost of national defense before 1972 (when the draft was ended) to the cost after 1972?
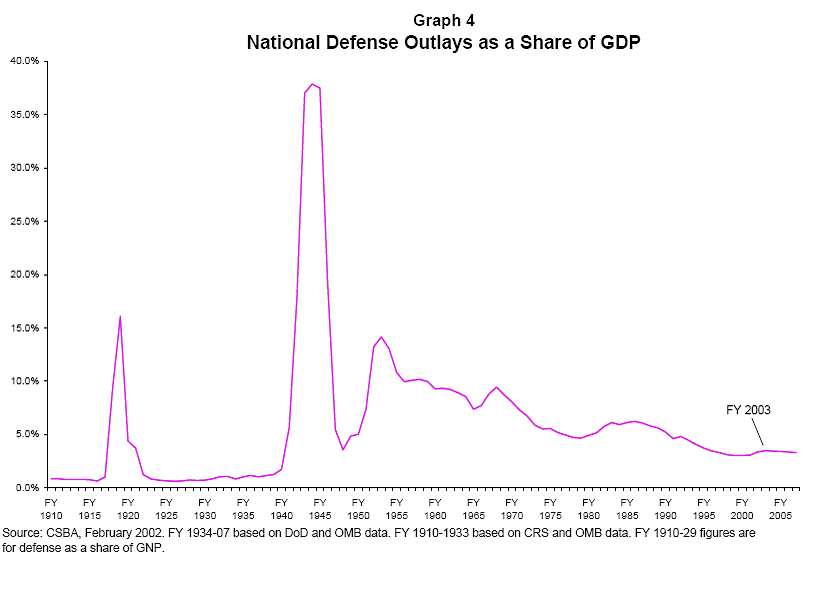
The true cost of
national defense pre 1972 was higher than reported, while the true cost post
1972 was the monetary cost. Here’s graph
of Defense as a share of GDP. The trend
since 1955 is downward, but the actual share should be higher.
2. “It will always cost more to increase output in the short run than in the long run.” Explain using isoquant and isocost curves.
True. In the long run, all inputs are variable so
the firm can move to the lowest isocost line. In the short run, the firm is
stuck with the capital stock it has in place and must produce at a higher cost
if output expands.
3. Input prices for a firm are w=4 and r=1 and
the production function is q = 4K.5 L .5 . What is the the least cost input combination
required to produce 40 units of output?
Suppose capital was fixed at 16 units.
What would be the implications for labor usage and of total costs?
To produce
40: 40 = 4K.5 L .5
Or 10 = K.5 L .5
We know that w/r =
4/1 = MRTS = MPL/MPK and MPK = 2K-.5
L .5 and MPL = 2K.5 L-.5
Which means that 4/1 = (2K.5 L-.5 )/( 2K-.5
L .5 ) => 4/1 = K/L and
K = 4L
Substitute into
the production function: 40 = 4(4L).5
L.5 = 16L and L = 40/16 =
Or
MPK = dQ/dK = .5
(4K.5 L .5 / K) = 2Q/K
and MPL = dQ/dL =
.5 (4K.5 L .5 /L )= 2Q/L
So MPL/MPK =
L/K and L/K = w/r = 4/1
so L/K=4 and L = 4K