Theses
Geometry of River Networks
PhD, Massachusetts Institute of Technology, 2000
arXiv page | arXiv version | local version
Supervisor: Dan Rothman
Department of Mathematics
Department of Earth, Atmospheric, and Planetary Sciences (unofficial)
Abstract:
Networks are intrinsic to a broad spectrum of
complex phenomena in the world around us:
thoughts and memory emerge from
the interconnection of neurons in the brain,
nutrients and waste
are transported through the cardiovascular system,
and social and business networks link people.
River networks stand as an archetypal example
of branching networks, an important sub-class
of all network structures.
Of significant physical interest in and of themselves,
river networks thus also provide an opportunity
to develop results which are
extendable to branching networks in general.
To this end, this thesis carries out a thorough examination
of river network geometry.
The work combines
analytic results, numerical simulations of
simple models and measurements of
real river networks.
We focus on scaling laws which are
central to the description of river networks.
Starting from a few simple assumptions
about network architecture, we derive
all known scaling laws showing that
only two scaling exponents are independent.
Having thus simplified the description
of networks we pursue the precise measurement
of real network structure and
the further refining of our descriptive tools.
We address the key issue of
universality, the possibility that
scaling exponents of river
networks take on specific values
independent of region.
We find that deviations from
scaling are significant enough
to preclude exact, definitive measurements.
Importantly, geology matters as
the externality of basin shape
is shown to be part of the reason
for these deviations.
This implies that theories that do not
incorporate boundary conditions
are unable to produce realistic
river network structures.
We also extend a number of scaling
laws to incorporate fluctuations
about simple scaling.
Going further than this,
we find we are able to identify
joint probability distributions
that underlie these scaling laws.
We generalize a well-known
description of the size and
number of network components
as well as a description of
network architecture, how
these network components fit together.
Both of these generalizations
demonstrate that
the spatial distribution
of network components is random and,
in this sense, we obtain
the most basic level of
network description.
On the Thermodynamic Formalism for the Farey Map
Masters, University of Melbourne, Australia, 1995
arXiv page | arXiv version | local version
Supervisor: Thomas Prellberg
Department of Mathematics
Department of Physics (unofficial)
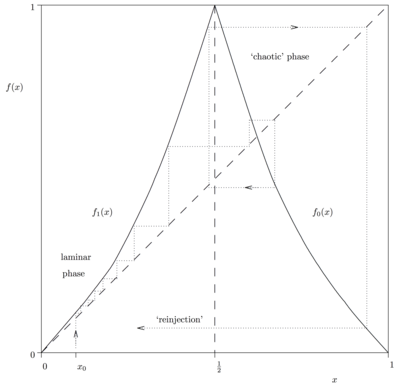
Abstract:
The chaotic phenomenon of intermittency is modeled by
a simple map of the unit interval, the Farey map.
The long term dynamical behaviour of a point under iteration of
the map is translated into a spin system via symbolic dynamics.
Methods from dynamical systems theory and statistical mechanics
may then be used to analyse the
map, respectively the zeta function and the transfer operator. Intermittency is
seen to be problematic to analyze due to the presence of an `indifferent
fixed point'. Points under iteration of the map move away from this point
extremely slowly creating pathological convergence times for calculations.
This difficulty is removed by going to an appropriate induced subsystem,
which also leads to an induced zeta function and an induced transfer
operator. Results obtained there can be transferred back to the
original system.
The main work is then divided into two sections. The first demonstrates
a connection between the induced versions of the zeta function and the
transfer operator providing useful results regarding the
analyticity of the zeta function.
The second section contains a detailed analysis of the pressure function
for the induced system and hence the original by considering bounds
on the radius of convergence of the induced zeta function.
In particular, the asymptotic behaviour of the
pressure function in the limit β, the inverse of `temperature',
tends to negative infinity is determined and the existence and nature of
a phase transition at β=1 is also discussed.